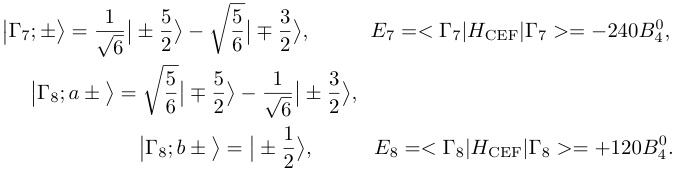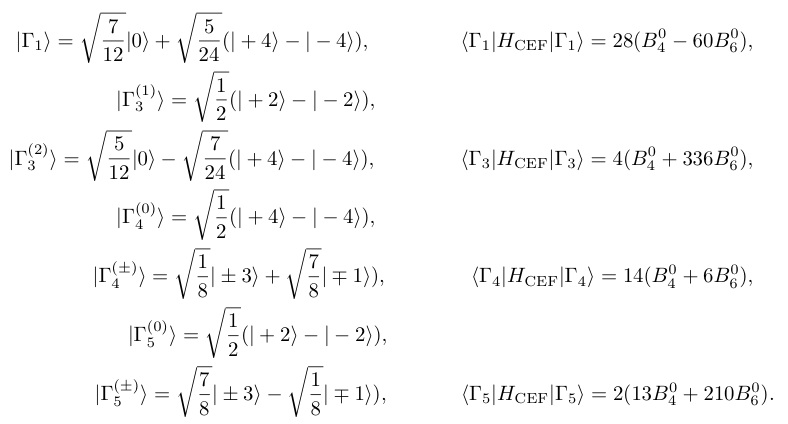本稿は、新学術領域研究（研究領域提案型）「重い電子系の形成と秩序化」が主催した「重い電子系若手秋の学校’１１」のテキストブックをHTML化したものです。

第３章　超音波実験の測定手法

 

3.6 重い電子系に対する超音波実験

続いて，$f$電子の遍歴性が強く，混成効果が効いている重い電子系に対する超音波実験について述べる．CeCu$_6$やCeRu$_2$Si$_2$等のスピン自由度に由来する近藤効果が効いている系では，一般的に多体効果の影響は全対称表現$¥Gamma_1$に対応するバルクモジュラスに現れ，対称性を低下させる横波弾性定数には現れない．一方，Coxらが提唱する非クラマース$¥Gamma_3$二重項に対する近藤効果である四極子近藤効果などのマルチチャンネル近藤効果ではその異方性を反映して横波弾性定数に$-¥log T$の温度依存性が現れるなどの理論予測がある[40]．後者のマルチチャンネル近藤効果の実験的検証はまだ中途の段階にあるので，ここでは従来型の磁気近藤効果由来の重い電子系に於ける縦波弾性定数の温度依存性の典型例を示そう.

先ずはL$¥ddot{¥rm u}$thi先生の超音波電子物性の教科書から一枚の絵を抜粋する．これは重い電子系の縦波超音波の典型を表した模式図である．３つの領域に分けて説明しよう．

図18 典型的な重い電子系の縦波弾性定数の温度依存性

(1) $T > ¥Theta_D$の高温領域とバックグラウンド

電子-格子相互作用の影響が無い場合，弾性定数は降温と共にほぼ線形に上昇する．もし，調和近似を基にフォノン間の相互作用を考えなければ，弾性定数は温度に依存せず一定となり，熱膨張は存在しない．しかし，一般的に弾性定数は昇温と共に減少し（軟化し），固体は膨張する ．それは調和近似の破綻を意味する．現実の系では非調和項の影響から$T > ¥Theta_D$の温度領域で弾性定数のバックグラウンドは$-T$に比例した温度依存性を示す．$T = 0$でそのバックグラウンドは$-T^4$に比例して低温で一定値に収束する．（図の点線）これはデュロン・プティ則により格子比熱が$T^3$に比例（即ち，内部エネルギーが$T^4$に比例）することに対応している．$-T^4$の温度依存性が成り立つ温度領域を決めるのは一般的に難しく，その温度依存性は現象論的に

(25)

と表す事ができる[41]．($s, t$は任意の定数)

(2) $T ¥sim ¥Delta$の結晶場効果

結晶場レベルの分裂幅$¥Delta$に対応した温度領域で，四極子感受率に起因するソフト化が生じる．例えば立方晶O$_{¥rm h}$群に於いて縦波弾性定数$C_{11}$は，バルクモジュラス$C_{¥rm B}$と$¥Gamma_3$対称性の$(C_{11}－C_{12})/2$モードの線形結合の形で$C_{11}$=$C_{¥rm B}$+4/3$(C_{11}-C_{12})/2$と表されるので，$¥Gamma_1$対称性の電気十六極子$(O_4^0+5O_4^4)$と，$¥Gamma_3$対称性の四極子$O_2^2$の感受率があらわれる．

(3) $T < T^¥ast$の強い電子-格子（グリューナイゼンパラメータ）結合¥¥

重い電子系では，$T < T^¥ast$において音響フォノンによる準粒子の散乱が無視できなくなる. （$T^¥ast$は多体効果の特性温度で磁気近藤効果の場合$T^¥ast ¥sim T_{¥rm K}$と考えてよい．）それが起源となった強い電子-格子相互作用によりポテンシャル変形が生じ，体積変化に対応する縦波モード（即ち$¥Gamma_1$対称性の歪み$¥epsilon_Β = ¥epsilon_x+¥epsilon_y+¥epsilon_z$に対応するバルクモジュラス$C_B$を含むモード）において弾性異常が現れる．この効果は一般的に対称性を低下させる歪みに対応する横波モードには現れない．この音響フォノンと準粒子の結合はグリューナイゼン定数によって現象論的によく説明できることが知られている．グリューナイゼン定数は熱力学的関係式$(¥frac{dT}{d¥epsilon})_S = (¥frac{¥partial T}{¥partial S})_{¥epsilon}(¥frac{¥partial S}{¥partial ¥epsilon})_T$から以下のように定義される（$S$はエントロピー）

(26)

ここで，$α_{¥rm T}$は等温過程における熱膨張係数，$C_{¥rm B}$はバルクモジュラスで等温圧縮率$¥kappa$の逆数として定義される． $C_{¥rm V}$は定積比熱である．図19と図20にそれぞれCeCu$_6$とCeRu$_2$Si$_2$の弾性定数の温度依存性を示す[42,43]．CeCu$_6$は220 Kに斜方晶から単斜晶への構造変化に伴うソフト化が横波$C_{66}$モードに観られる[43]．より低温領域では明瞭な結晶場効果が縦波$C_{11}$, $C_{22}$, $C_{33}$と横波$C_{44}$に現れ，低温で収束するが，$T < 5$ Kで近藤一重項の形成が始まるにつれ，$C_{11}$は低温でさらにもう一段階ソフト化を示す[44]．CeRu$_2$Si$_2$は対称性を低下させる横波モードに明瞭な結晶場効果は観られず，体積歪みに関連した縦波モード$C_{11}$, $C_{33}$に特に顕著なソフト化が観られる．このような体積歪みに関係した縦波モードのみに現れる弾性異常は$4f$電子が遍歴し準粒子バンドを形成していると考えられているCeSn$_2$, CeNi, CeNiSnなどにも共通して観られる．

図19 CeCu$_6$の弾性定数の温度変化 [43]

図20 CeRu$_2$Si$_2$の弾性定数の温度依存性 [42]

結合定数$¥Omega$が正で大きな値を持つ場合，近藤一重項が形成されると共に体積収縮が起こることが熱膨張測定などで確かめられている．これをKondo Volume Collapseという．$T = 0$におけるその体積変化の大きさは多体効果の特性温度$T^¥ast$(近藤温度のオーダー）を用いて

(27)

と見積もることができる．ここで$n$は単位体積あたりの磁性イオンの数であり，$n ¥sim 10^{28} [m^{-3}]$程度であるとする．重い電子系において実験的に求められたグリューナイゼン定数の典型的な値は$¥Omega ¥sim 100$程度，多体効果の特性温度を$T^¥ast ¥sim 10$ [K], ボルツマン定数$k_{¥rm B} = 1.38 ¥times 10^{-23} $[J K$^{-1}$], バルクモジュラスを$C_{¥rm B} ¥sim 10^{11}$ [J m$^{-3}$]とおくと，体積歪みの大きさは$¥epsilon_{¥rm V} ¥sim 10^{-3}$となり，研究室レベルのX線装置でも検出できるような，かなり大きな変化であることがわかる．実際にCeRu$_{2}$Si$_{2}$で格子定数の変化が観測されており，$T ¥to 0$の外挿値は$¥epsilon_V ¥sim 1.4 ¥times 10^{-3}$程度と見積もられ[45]，上式で良く再現される．
一方，URu$_2$Si$_2$やUPt$_3$などアクチノイド系の重い電子系では上記のグリューナイゼン定数による弾性応答が成り立たない例も報告されている[42,46,47]．これらの系では超音波の周波数が電子散乱時間に近づき，超音波の伝搬において断熱近似が成り立たなくなっていることが推測され，エネルギー散逸を考慮した等温弾性率を用いた特別なアプローチが必要である．

(第4章に続く）

本稿は、新学術領域研究（研究領域提案型）「重い電子系の形成と秩序化」が主催した「重い電子系若手秋の学校’１１」のテキストブックをHTML化したものです。

第３章　 歪みと弾性定数，四極子感受率

物理的に意味があるのは音速ではなく，単位体積当たりに蓄えられる弾性エネルギーを表す「弾性定数」である．実験からは音速とC = ρ v²の関係で弾性定数（SI系では[J m^-3]，CGS単位系では[erg cm^-3]の次元）が得られる．物質の密度ρが一定であると仮定した時，弾性定数の絶対値は音速の絶対値によって決まり，ヤーン・テラーエネルギーや四極子相互作用の結合定数を見積もる際に重要になる．一方，弾性定数の単位を圧力の単位[Pa]や[dyn/cm²]で表す場合もある．こちらは圧力効果を論じる場合や圧縮率（バルクモジュラス）との比較を行う際に有効かもしれない ．

本章ではまず局在性が強い（混成効果が弱い）f 電子系について四極子感受率の定式化を行う．結論を先に言ってしまうと，それは量子力学の二次摂動を用いた，電気双極子と誘電率，あるいは磁気双極子と帯磁率の関係式と全く同じである．超音波が作る歪み場と結合するのは電気四極子であるから，波動函数に適用する演算子のランクが双極子から1つだけ上がり，物理量がベクトルからテンソルに変わる以外は何ら特別なことは無い．だから一度でも感受率の計算をやったことのある方は読み飛ばしてもらって構わない．

3.1 歪みと弾性エネルギー

物質は外場に対して何らかの応答を示す．例えば，磁場H に対して磁束密度B，電場E に対して電束密度D，応力Tに対して歪みS が発現する．それらの関係を表１に示す．

Table 1 物理テンソル・特性テンソル・外場のトライアドと，応答する多極子

一般に固体物理学で結晶が物理テンソル I の場の下にある場合，それによる観測量eと結晶の性質に由来する（結晶の異方性によって簡略化された）特性テンソルdの間には以下の関係がある．

(1)

ここで，添え字i, j (=1,2,3)は座標成分を表し，添え字の数は階数(ランク)と呼ぶ．
１階ランクのテンソル（即ちベクトル）同士を結びつける物理量d_ijは２階ランクのテンソルであり，マトリクス型式で表される．

(2)

さて，超音波による音速測定から得られる物理量は表1の弾性（スティフネス）定数である．これは物質の応力に対する歪みにくさ，即ち「かたさ」に対応する量で，歪みSも応力Tも2階ランクの極性テンソルであるから，これらを繋ぐ特性テンソルの弾性定数は4階ランクの極性テンソルである．

(3)

応力T_ijはi面に働くj方向の力をあらわす．本稿では今後，誘電率は登場しないので，普段私たちが論文で用いている表記に変更し，歪みをε_kl，応力をσ_ijと再定義すると

(4)

テンソル量C_ijklは対称で，その要素は添字の順番に依らないから，以下のようなVoigtの表記で書き換えることができる.

11 → 1, 　22 → 2,　33 → 3,　23,(32) → 4,　31(13) → 5,　12(21) → 6.

マトリクス形式で式(4)を表してみよう．

(5)

ここで，空白部分は対称要素C_ij=C_jiであるため省略した．さらに，物体に働く応力は釣り合っており，回転モーメントは無いとすると，応力も歪みも対称となり，もともと3⁴ = 81個あった4階テンソルの要素の数が21個に簡約化される．さらに結晶がある対称操作に対して不変であるとすると，特性テンソルは簡約化される．独立な弾性定数の要素は結晶の対称性に応じて減り，最も対称性の高い立方対称では独立な弾性定数はC₁₁, C_12, C₄₄のたった３個になる．ここでは群論の詳細については割愛するが，三斜晶から立方晶までの結晶対称性において対称操作によって残る独立な弾性定数と，その基底函数をまとめたものを表2に示す.

Table 2. 様々な結晶系における独立な弾性定数 [6]

Table 3. 立方晶系における超音波の伝搬・変位方向と弾性定数の関係

下では簡単のため，結晶構造が立方晶の場合について考える．一般に，歪みは次のような対称テンソルで定義される．

(6)

ここでu_iは変位ベクトルであり，歪みは無次元量であることがわかる．上式で定義された歪みは，x, y, zの二次多項式と同じ変換をする(i,j=1,2,3 → x,y,zと置き直すと解り易い)から，点群Oの既約表現と同じ変換をする対称歪みε_Γを求めることができる．表3に立方晶系における超音波の伝搬・変位方向と，誘起される歪み，観測される弾性定数の関係を示した．立方晶系の弾性エネルギーはフックの法則により，弾性定数と対称化された歪みを用いて以下のように書ける．

(7)

ここでC_B = (C₁₁+2C₁₂)/3はバルクモジュラス で結晶対称性を保持するΓ₁ 対称性の体積歪みε_B = ε_xx+ε_yy+ε_zzに対応し図4に示すような単極子・電気十六極子と結合する．(C₁₁-C₁₂)/2, C₄₄はそれぞれΓ₃, Γ₅対称性の対称歪みに対する四極子の応答に対応する．磁場中の横波超音波には歪みに加えて，格子の回転が弾性エネルギーに寄与する．そのため超音波の伝搬方向と磁場方向の関係に依っては，弾性エネルギーに差が生じる．本稿では割愛する．

(第３章3.2節に続く）

本稿は、新学術領域研究（研究領域提案型）「重い電子系の形成と秩序化」が主催した「重い電子系若手秋の学校’１１」のテキストブックをHTML化したものです。

第３章　歪みと弾性定数，四極子感受率

 

3.3 立方晶系に於けるCe³⁺ , Sm³⁺ (J = 5/2), Pr³⁺ , U⁴⁺(J =4) の四極子感受率

上記の四極子感受率をJ = 5/2とJ = 4の場合について計算した結果を示し，四極子自由度を有する典型的な希土類化合物の弾性定数と比較してみよう．

(1) J = 5/2

f電子軌道が安定で局在している場合（混成や価数揺動等が無く，結晶場基底状態がLS多重項で記述できる場合）を考える．先ず半整数の角運動量Jを持つ系を考える．Ce³⁺やSm³⁺は半整数の角運動量J = 5/2をJ多重項の基底状態に持ち，立方晶系の結晶場ではΓ₇二重項とΓ₈四重項に分裂する．その波動函数と固有値は次の様に書ける．

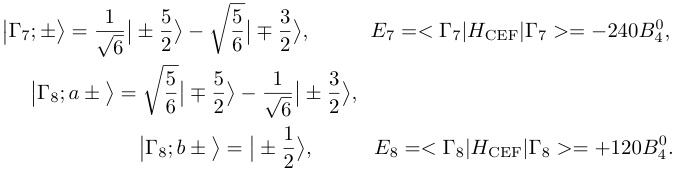
(23)

ここで|J = 5/2, J_z> = |J_z>とした．Γ₇はクラマース二重項であり，磁場によって分裂するが，歪み場では分裂しない．他方，Γ₈四重項は２つのクラマース２重項が縮退しており，磁気双極子のみならず，電気四極子・磁気八極子も合わせて4 x 4 = 16の自由度を持つ．（表４）

表4 O群の積表

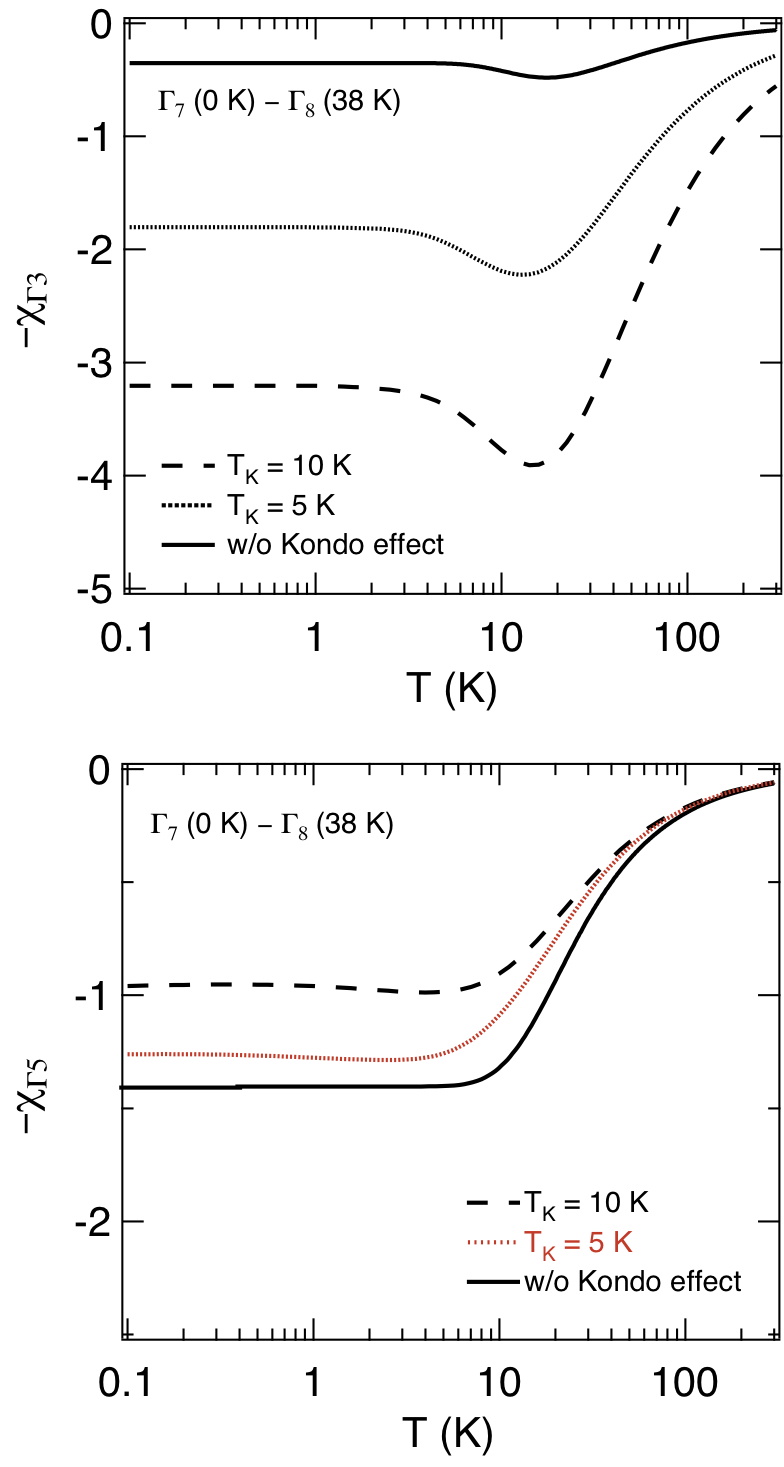
よって，Γ₈基底状態を持つCe, Sm化合物では四極子または八極子が秩序変数となり得るため，極めて興味深い多極子の物理が期待できる．超音波物理の観点からは基底状態がΓ₇かΓ₈であるかに従って，相異なる弾性定数の温度変化を示すことが期待されるため，分光学的に結晶場基底状態を決定できる．例として図5にJ = 5/2におけるΓ₇基底状態の場合とΓ₈基底状態の場合の四極子感受率を示す．それぞれ縦軸と横軸は結晶場分裂幅Δ [K]で規格化してある．ここでxはLea-Leask-Wolfの結晶場ハミルトニアンにおける変数xに対応する[7]．Γ₃対称性の歪みに対応する四極子感受率-χ_Γ3は四極子O₂²の応答であり，横波弾性定数　(C₁₁-C₁₂)/2に対応する．Γ₅対称性歪みに対応する四極子感受率-χ_Γ5は四極子O_yz, O_zx, O_xyの応答であり横波弾性定数C₄₄に対応する．Γ₇基底の場合，低温でヴァン・ヴレック項が支配的となり弾性定数は一定値に収束する．一方，Γ₈基底の場合は低温でキュリー項が支配的となり，1/Tに比例するソフト化が現れる．

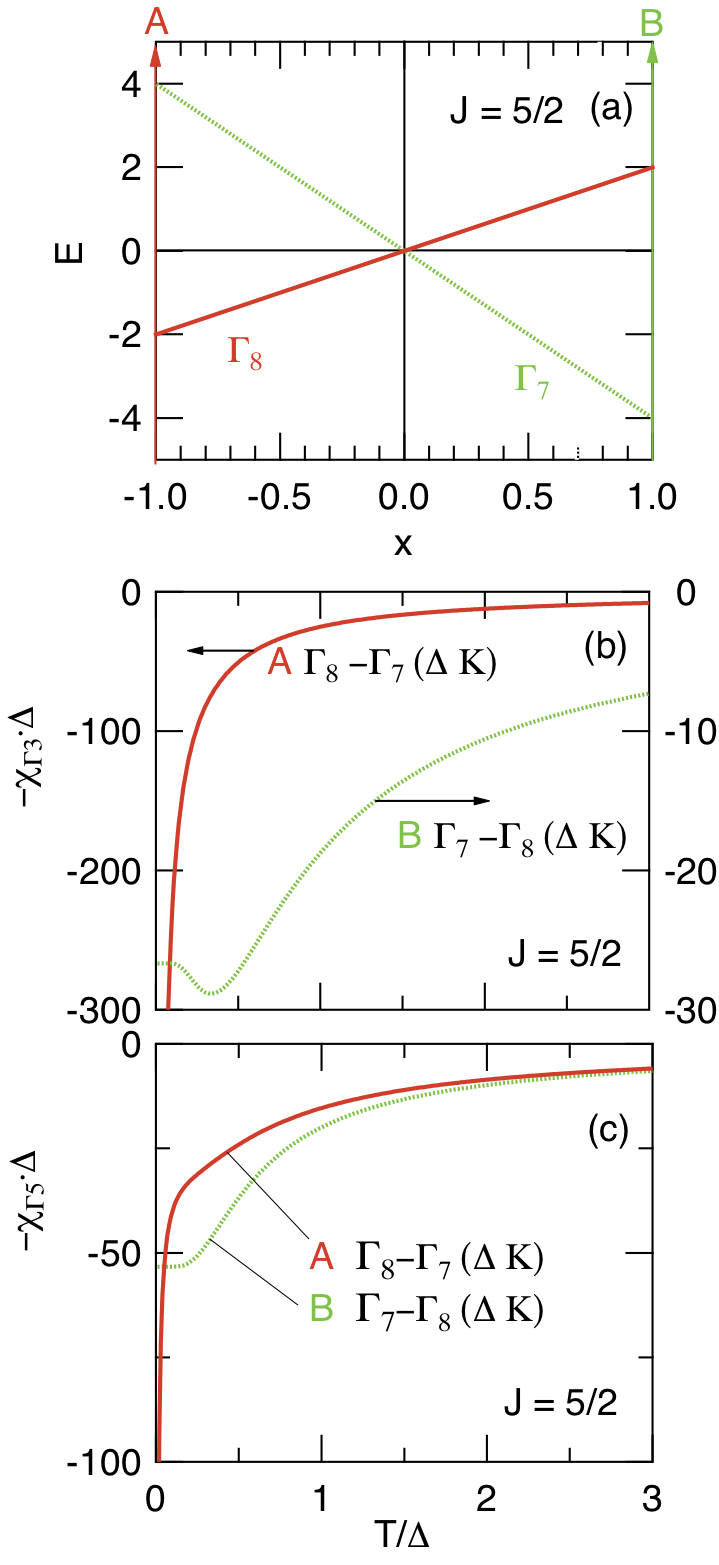
Fig. 5 (a) J = 5/2に対する立方晶系点群O_hの結晶場レベルスキーム (W = 1とおいた）.
結晶場A, Bを仮定した場合の;
(b) 四極子感受率-χ_Γ3の温度依存性,
(c) 四極子感受率-χ_Γ5の温度依存性
（縦・横軸共に第一励起状態の結晶場分裂幅Δでスケールした．）

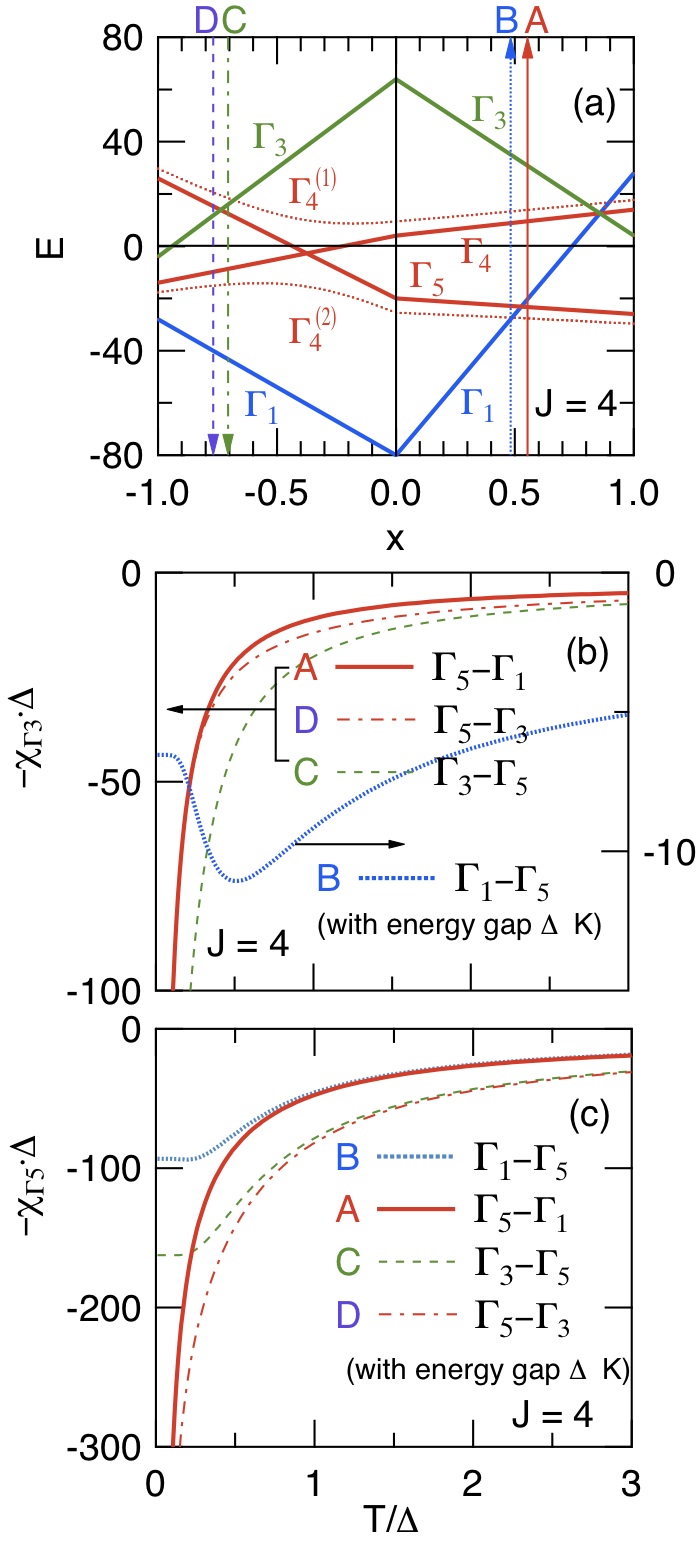
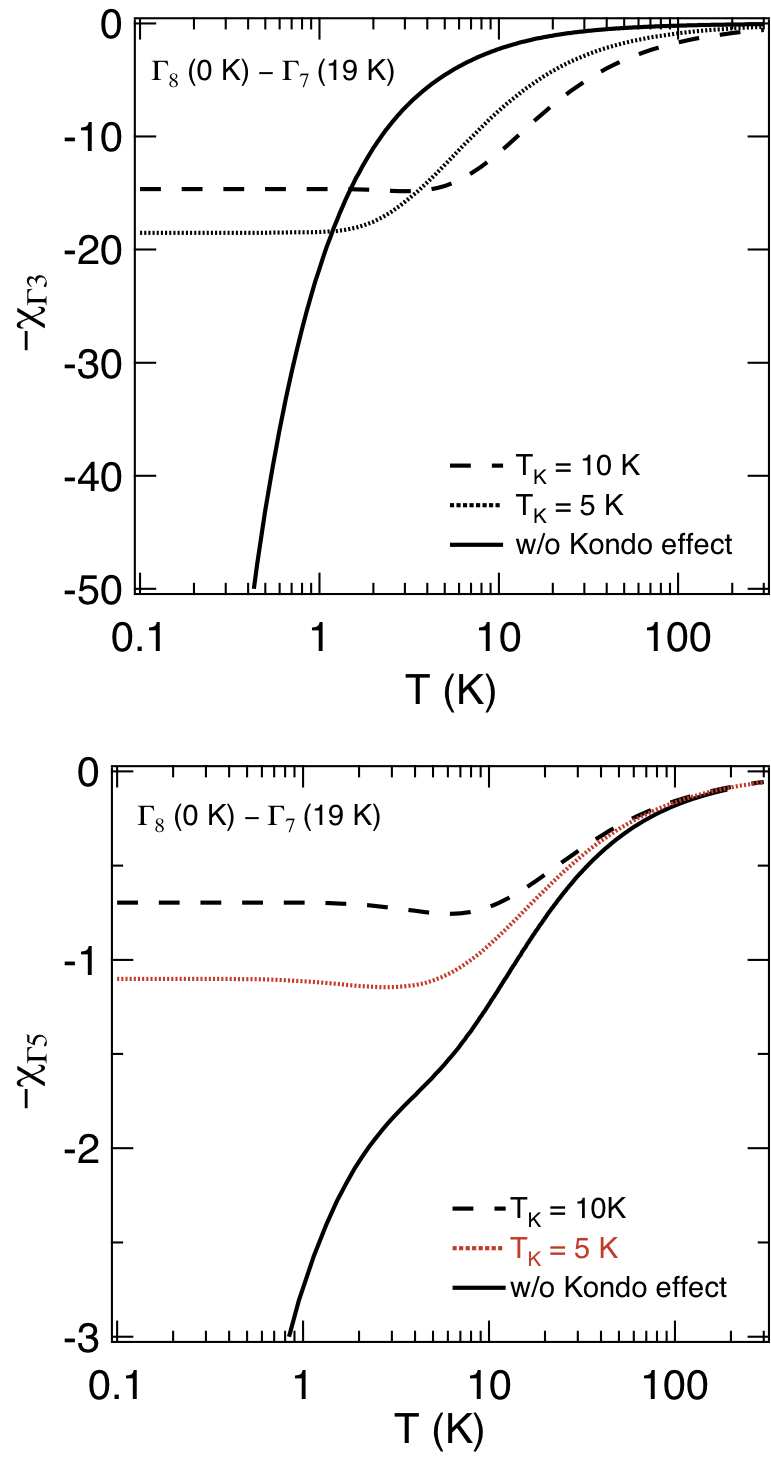
Fig. 6 (a) J = 4に対する立方晶系点群O_h (T_h :破線 )の結晶場レベルスキーム (W = 1とおいた) [16,17].
O_h群における結晶場A-Dを仮定した場合の;
(b) 四極子感受率-χ_Γ3の温度依存性,
(c) 四極子感受率-χ_Γ5の温度依存性
（縦・横軸共に第一励起状態の結晶場分裂幅Δでスケールした．)

(2) J = 4
次に，全角運動量Jが整数の場合を考えよう，J = 4の波動函数と固有値は以下の様に書ける.

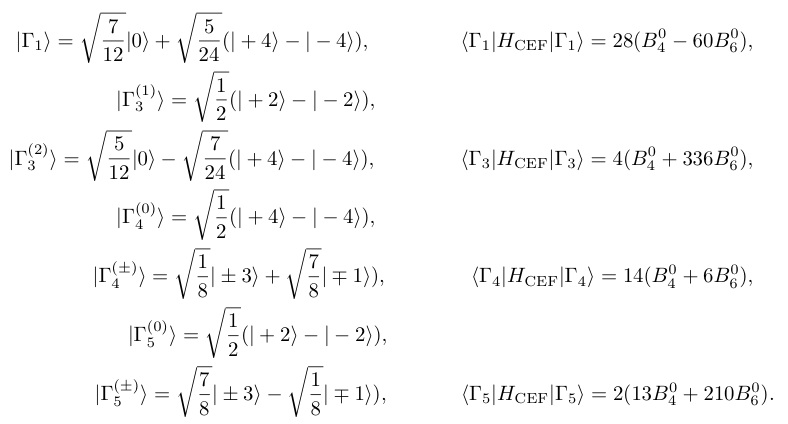
(24)

整数の角運動量を持つ希土類化合物も興味深い弾性的性質を示す．立方晶系においてΓ₃二重項の波動函数は，Γ₃対称性の電気四極子O₂⁰,O₂²の行列要素に対角成分を持つため，Γ₃対称性の四極子感受率に低温で1/Tに比例した結晶場によるソフト化が期待される．一方，磁気測定（帯磁率，中性子散乱）からは選択則(磁気双極子モーメントJ_x, J_y, J_zは立方晶系においてΓ_4uに属することを踏まえて表4のO群の積表を参照してみよう.)よりΓ₃二重項の応答が得られないため，超音波測定がΓ₃非クラマース系の研究において欠かせない道具となっている．超音波で観測される弾性定数(C₁₁-C₁₂)/2に対応する四極子感受率-χ_Γ3はΓ₃状態のキュリー項を敏感に検出できる．これまでPrPb₃, PrMg₃, PrPtBi, PrInAg₂, PrIr₂Zn₂₀などがΓ₃基底を持つ化合物として注目されている．そこでは四極子の不整合構造や四極子近藤効果，さらにΓ₃二重項が持つ磁気八極子T_xyzの効果など，様々な物理の議論が展開されている．

図6(b), (c)にJ = 4について様々な基底状態(T_h群の影響はΓ₄とΓ₅にのみ現れる．ここでは竹ヶ原らによる結晶場ハミルトニアン[16]の６次項(O₆²-O₆⁶)に付く変数yとして，PrOs₄Sb₁₂の結晶場解析で用いられた値y = 0.105を用いた.)を仮定した場合の四極子感受率の計算結果を示す．基底状態と第一励起状態の結晶場分裂幅Δで温度軸と縦軸を規格化してある．基底状態がΓ₃の場合-χ_Γ3は低温でキュリー項によるソフト化が現れ，-χ_Γ5は低温で一定値に収束するヴァン・ヴレック項が支配的となるため選択則によるコントラストが現れる．

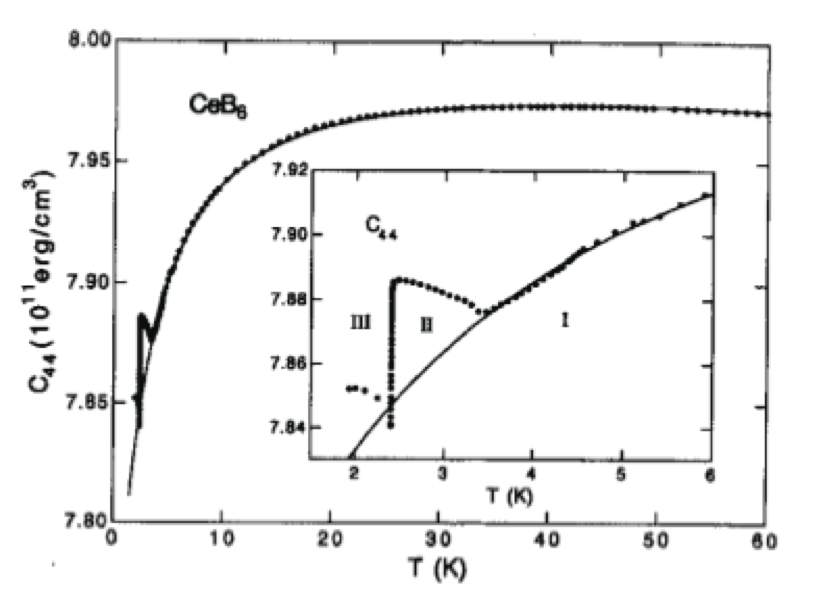
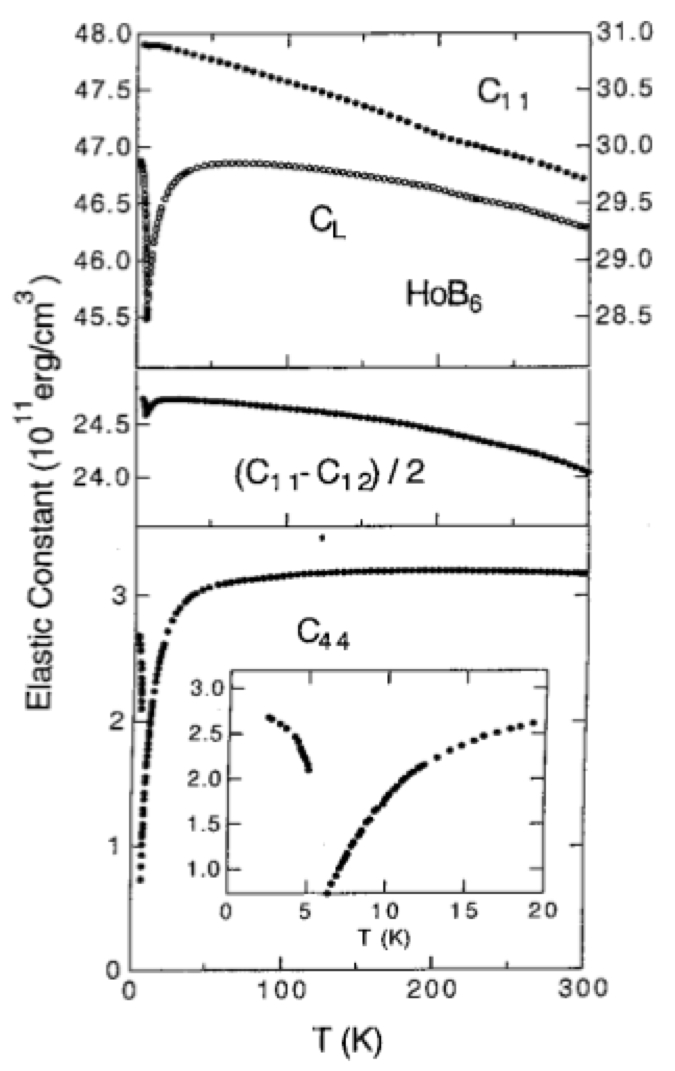
さて，典型物質の弾性定数と比較してみよう．図７にCeB₆の弾性定数を示す[18]．CeB₆は立方晶で，Ce³⁺イオン（J = 5/2)の結晶場基底状態はΓ₈(0 K)-Γ₇(540 K)であることがわかっている．弾性定数はΓ₈四重項を反映して(C₁₁-C₁₂)/2, C₄₄共に低温でキュリー項による1/Tに比例したソフト化が観測される．超音波実験によって決定されたC₄₄の四極子間相互作用係数はg'_Γ5= -2.2 Kと負の値をとり，O_yz, O_zx, O_xy型の反強四極子秩序を示唆する.

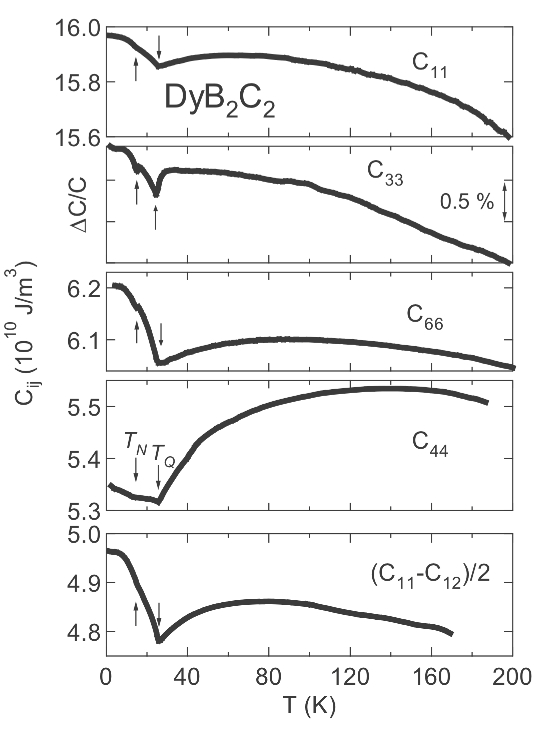
一方，J = 4の系で超音波が最もその威力を発揮するのは先述のΓ₃基底を持つ系であるが，本稿ではあえてPrOs₄Sb₁₂を挙げよう．この物質においてPrイオンのサイトシンメトリーはT h で，Γ₁-Γ₄⁽²⁾が約8 Kで擬縮退した擬四重項基底状態を持つことが解っている．実はこの物質が注目された当初は比熱，磁化の解析から基底状態はΓ₂₃（O_hにおけるΓ₃）二重項であると考えられていた[19]．図８と図９に弾性定数(C₁₁-C₁₂)/2とC₄₄の温度変化と，２つの結晶場モデルによる計算結果をそれぞれ示す．図8の内挿図を見ると，Γ₁基底を基にした四極子感受率の計算結果は3 Kで極小値をとってハード化するため，T_C = 1.85 Kまで弾性定数の減少が続く実験結果を再現できていない．このように零磁場の四極子感受率の解析では一見Γ₂₃基底の方が良く合っているように見える．しかし，それが誤りであることは弾性定数の磁場変化を測定すると明らかになる．図10に弾性定数(C₁₁-C₁₂)/2の磁場変化（H || <110>)と，基底状態のゼーマン分裂を考慮した四極子感受率の磁場変化をそれぞれの結晶場基底モデルについて示す[20,22]．するとそこでも結晶場モデルによって四極子感受率に明らかな差異が認められ，Γ₁基底のモデルが良く合うことがわかる．PrOs₄Sb₁₂は磁場誘起の四極子秩序を示すが，H || <110>において8 T付近で生じる準位交差がその起源となることからもΓ₁-Γ₄⁽²⁾の擬四重項基底状態であることが裏付けられる．それでは，なぜ実験結果は低温領域で四極子感受率に基づく計算から「ずれ」るのだろうか．その理由はPrイオンのオフセンター自由度を考えることによって説明される[21]．（詳細は5.3章で述べる．）

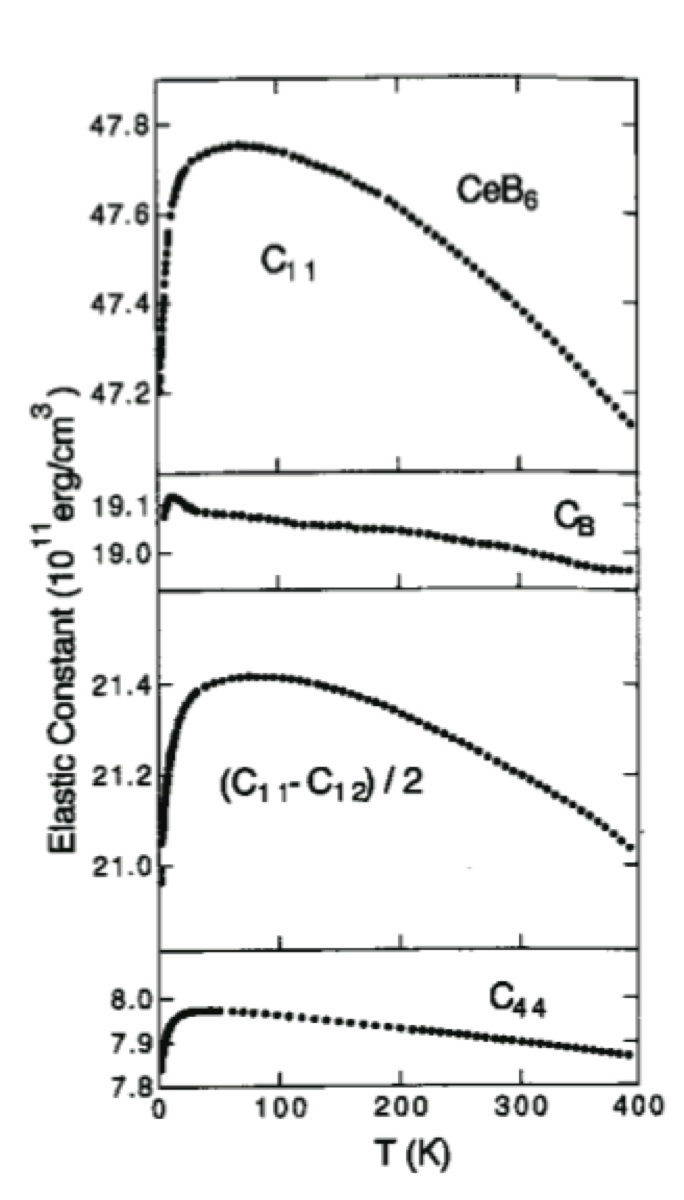
FIg. 7 CeB₆の弾性定数C₁₁, C_B, (C₁₁-C₁₂)/2, C₄₄の温度変化

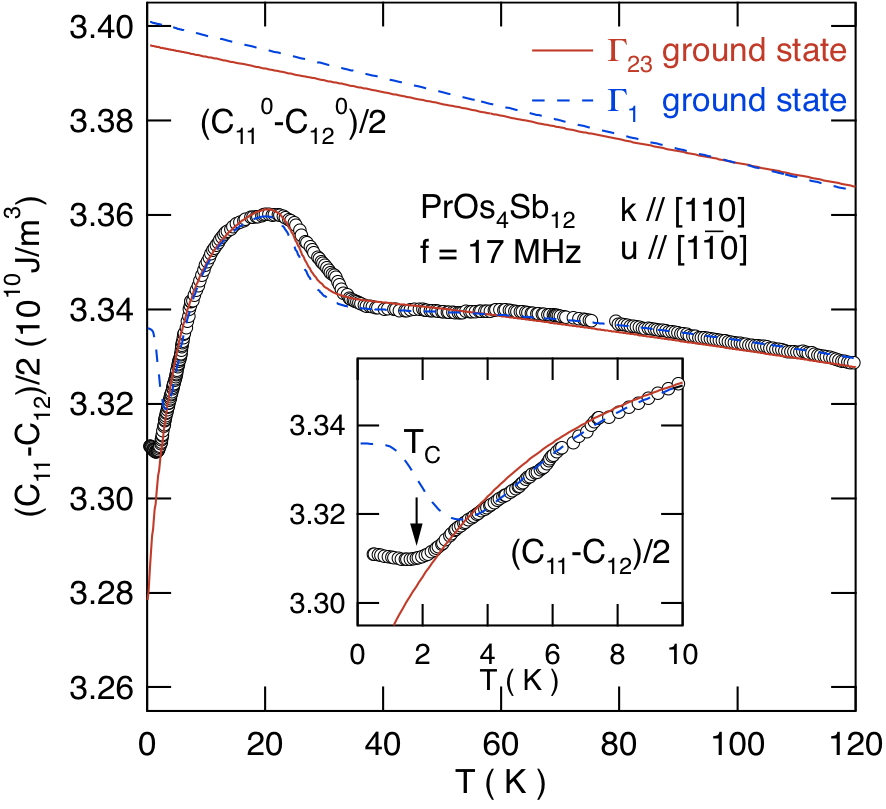
Fig. 8 PrOs₄Sb₁₂の弾性定数(C₁₁-C₁₂)/2の温度変化
(30 Kの弾性異常はラットリングに伴う超音波分散である．実線はΓ₁基底状態，破線はΓ₂₃基底状態を仮定した場合の四極子感受率による解析）[58]

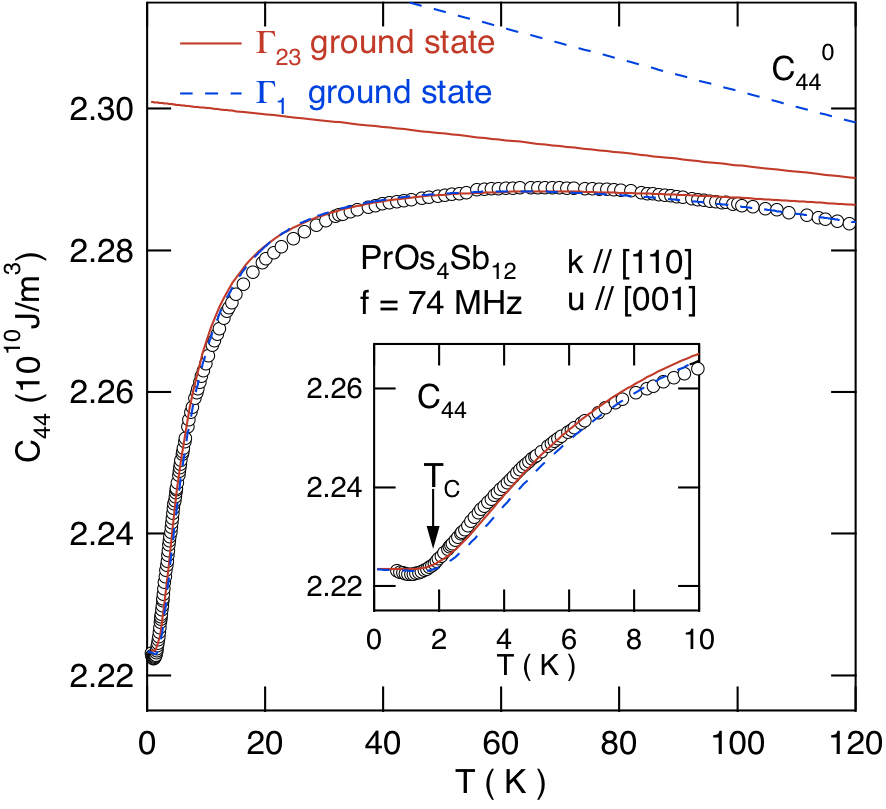
Fig. 9 PrOs₄Sb₁₂の弾性定数C₄₄の温度変化(実線はΓ₁基底状態，破線はΓ₂₃基底状態を仮定した場合の四極子感受率による解析）[58]

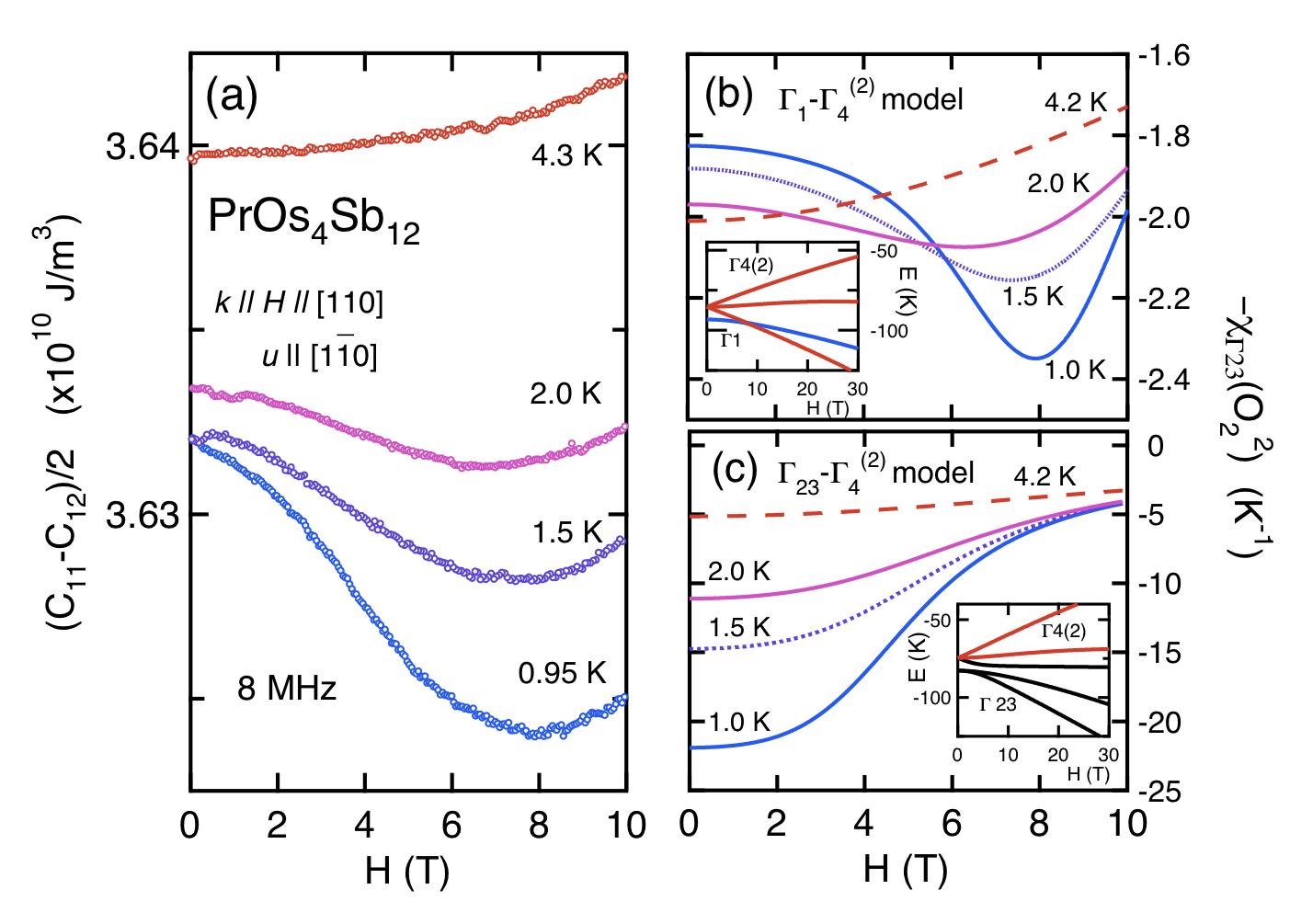
Fig. 10
(a) PrOs₄Sb₁₂の弾性定数(C₁₁-C₁₂)/2の磁場変化　(H || <110>).
(b) 結晶場基底状態にΓ₁-Γ₄⁽²⁾擬四重項を仮定した場合の四極子感受率-χ_Γ23の磁場変化 (-χ_Γ3と同義）.
(c) 結晶場基底状態にΓ₂₃-Γ₄⁽²⁾擬五重項を仮定した場合の四極子感受率-χ_Γ5の磁場変化.（それぞれ内挿図は結晶場レベルスキームの磁場変化）[22]

(第３章3.4節に続く）

本稿は、新学術領域研究（研究領域提案型）「重い電子系の形成と秩序化」が主催した「重い電子系若手秋の学校’１１」のテキストブックをHTML化したものです。

第4章　緩和の現象論

ここまで駆け足で，$f$電子化合物の弾性応答の典型例について紹介してきたが，これまでの議論に於いては，超音波による歪みは電子系に対する「静的な」摂動として取り扱った．超音波の周波数$¥omega$はたかだか数百MHz程度であるから，一般に電子系の緩和時間$¥tau$よりも充分長い（$¥omega ¥tau ¥ll 1$）．この場合，パルスエコー法の実験で得られる「音速」とは，図21に示すフォノンの分散関係における音響フォノンモードの$k = 0$の傾き，即ちフォノンの「群速度」

(28)

に該当する．
一方，相転移近傍における臨界現象や価数揺動，ラットリングに伴う局所電荷ゆらぎ等に起因し，電子系の緩和時間が超音波の周波数に近づく場合（$¥omega ¥tau ¥sim 1$）は, 電子-フォノン相互作用を通して音速（と超音波吸収）にも緩和現象が現れる．ここで位相速度を

(29)

と定義すると，音速に分散がある場合，群速度と位相速度が一致しなくなることを意味する．これを「分散領域」と呼ぼう．以下の議論では分散領域($v_{¥rm g} ¥neq v_{¥rm p}$)において周波数$¥omega$に依存する位相速度$v_{¥rm p}$を考える．また，$C = ¥rho v^2$の関係式で結ばれる弾性定数（弾性率）も周波数に依存する動的弾性定数（弾性率）$C(¥omega)$として定義できる ．それは複素弾性率の実数成分として現象論的に理解できる．以下にはその一般式を示す．

図21 左はカゴ状物質における低エネルギー領域のフォノン分散関係の模式図．右は群速度$v_{¥rm g}$と位相速度$v_{¥rm p}$の概略図（ここでは$k ¥sim 0$近傍の曲率の変化を誇張して描いている）．

4.1 複素弾性率

熱平衡状態に外部から磁場$H$, 電場$E$, 歪み$¥epsilon$, 温度$T$などをかけて平衡状態からずらすとき，再び熱平衡状態に近づいていく過程を緩和現象という．平衡状態と瞬間力が「静的」な内部状態であるのに対して，緩和現象ではさらに系の「動的」な性質を記述する必要がある. 例えば熱力学では状態方程式等を与えて系の性質を規定しなければならないように，動的な現象論では緩和（応答）函数をまず与えてから系の状態を規定していかなくてはならない．

たとえばある秩序変数$¥eta$を仮定し，それが歪みや応力といったマクロな物理量の影響を受ける場合を考える~¥cite{45}．非平衡状態で$¥eta$は時間と共に変化し，平衡値$¥eta_0$に近づいてゆく．この緩和過程を表す最も簡単な場合は

(30)

と記述できる．$¥tau$は典型的な緩和時間である．平衡値$¥eta_0$も同様に歪みの影響を受ける．上式は$t = 0$で$¥eta = ¥eta'$であったとすると，

(31)

のように指数函数的に系の緩和が起こる事を表している．緩和函数（または応答函数）が時間と共に指数函数的に減衰する例は自然界にしばしば観られ，特に誘電体の誘電緩和現象で起きるデバイ型緩和現象は，磁化の緩和を観る交流磁化率や局所電荷ゆらぎの緩和を観る超音波分散の解析に類推して用いられる．

さて，系に音波が伝搬することにより歪みが弾性波の角周波数$¥omega$で周期的に断熱変化すると仮定する．

(32)

すると，秩序変数の平衡値$¥eta_0$も弾性波の影響を受けるが，$¥eta$もまたある位相差を伴って変化するはずである．
その結果，式(30)は

(33)

と書け，

(34)

となる．
弾性率は一般的な感受率(応答/外場)として理解すると(応力/歪み)$= ¥partial¥sigma / ¥partial¥epsilon$で与えられる~¥cite{46}．

(35)

ここで第１項は静的弾性率，第２項は動的弾性率である．
式(33)を代入すると

(36)

ここで，
$(¥partial¥sigma/¥partial¥epsilon)_{¥eta}+(¥partial¥sigma/¥partial¥eta)_{¥epsilon}(¥partial¥eta/¥partial¥epsilon)$
は充分に遅い緩和に対する応力の歪み微分であるから，歪みの変化が充分に遅い緩和過程($¥omega ¥tau ¥ll 1$)で平衡状態が壊れないとすると$¥eta$は常に平衡値$¥eta_0$をとるため，単純に$(¥partial¥sigma/¥partial¥epsilon)_{eq.}$と書ける．ここで

(37)

を低周波極限（即ち静的弾性率）と定義する．
一方，歪みの変化が非常に速い場合($¥omega ¥tau ¥gg 1$)では$¥eta$は系の変化に追いつけずに一定$¥eta_{¥infty}$に保たれる．その中間の周波数つまり$¥omega ¥tau ¥sim 1$の近傍では$¥eta$の変化は歪みのそれよりも位相が遅れ，応力の変化として観測される．ここで

(38)

を高周波極限と定義する．
式(37) と(38)を用いると，(36)は

(39)

と書ける．

先述の通り，$¥chi$は弾性率に限らず，一般的に交流磁化率や誘電緩和などの緩和現象を解析する感受率と類推できる．現実を描写するため，弾性率を実部と虚部に分ける．複素弾性率$¥chi^{¥ast}$と複素音速度$v^{¥ast}$の関係式

(40)

と，複素音速度と吸収係数αの関係式

(41)

より，実際の超音波測定では複素弾性率$¥chi^{¥ast}=¥chi_{¥rm Re.}+i ¥chi_{¥rm Im.}$の実部は動的弾性定数$C(¥omega)$，虚部は超音波吸収係数$¥alpha(¥omega)$として観測される．

(42,43)

図22は充填スクッテルダイトLaOs$_4$Sb$_{12}$の超音波分散の研究で得られた活性エネルギーと緩和時間を用いて計算された動的弾性率（左軸）と超音波吸収係数（右軸）である．図22の下に示すのはアレニウス型の緩和時間の温度依存性である．超音波の測定周波数$¥omega$（左軸から延ばした直線）と系（ラットリング）の緩和時間$¥tau$がマッチングする領域（共鳴条件$¥omega ¥tau ¥sim 1$）で，実部の弾性率は低周波極限$C_0$から高周波極限$C_{¥infty}$へ増大し，虚部の超音波吸収は極大を示す．これが次章で示すラットリングに伴う超音波分散の現象論的な解釈である．

図22 LaOs$_4$Sb$_{12}$の超音波分散の現象論的な解釈.

4.2 音響フォノンと音速の関係（位相速度と群速度についての蛇足）

先述した通り，パルスエコー法で得られる音速とは，非分散領域（音速に分散が無い領域）においては，超音波パルスの波束の間隔 [s]と伝搬経路長[m]から求められる速度を意味し，これはフォノンの群速度$v_{¥rm g}$に該当する．一般に音速という場合はこれを指すことが多い．一方，位相比較法で得られる「音速」とは，一定の位相をもった波面が伝搬する速度のことを指し，これはフォノンの位相速度$v_{¥rm p}$に該当する．先述の通り，実際の測定では一定位相を持つ連続波をパルス化して入射しており，入射波束が持つ位相と基準信号の位相差を検出し，位相差を一定（即ち波数$k$を一定）に保つように周波数$¥omega$に負帰還をかけ，位相速度の相対変化$¥Delta v_{¥rm p}(¥omega)/v_{¥rm p}(¥omega)$を周波数の相対変化$¥Delta ¥omega/¥omega$として読み替えている．分散領域では群速度と位相速度が一致しない($v_{¥rm g} ¥neq v_{¥rm p}$)が，非分散領域では一致する($v_{¥rm g} = v_{¥rm p}$)ため，位相比較法は両者を測定していることになる．

ここで慧眼なる読者は気づかれたかもしれないが，結晶にモノクロマティックな（単一周波数を持った）超音波を入射する場合，分散領域ではある周波数$¥omega$に対応するフォノンの位相速度が変化し，超音波が伝搬しなくなることが懸念される．例えば図22にあるように，緩和時間がアレニウス型の温度依存性を示す時，厳密にモノクロマティックな超音波を用いた実験を行った場合，群速度と位相速度が異なるので，パルスエコー間隔を追った実験では緩和に伴い位相速度が変化し，パルス波の大部分が吸収されるため，音速の低周波極限から高周波極限への変化は不連続なデータとして観測されるはずである．しかし，実際は超音波トランスデューサの特性上，ある帯域幅を持った波群が入射されているため，我々が実験で作り出せる超音波は完全なモノクロ波ではない．よって，分散領域でも音速の相対変化をある程度連続的に追う事ができる．位相比較法では分散領域において位相速度が変化しても，周波数分布の裾の周波数帯の波が伝搬し続けるので，位相信号を見失う事無く追跡し，負帰還によって変調される周波数の相対変化から位相速度の相対変化を観測することができる．

(第5章1節に続く）

第5章　超音波からみたラットリング

5.4 これまでに超音波測定から得られたオフセンターラットリングの傍証

これまでに紹介した$Ln$$_3$Pd$_{20}$Ge$_6$と$Ln$Os$_4$Sb$_{12}$ ($Ln$ = 希土類)カゴ状化合物に於いて，超音波測定で観測される超音波分散と低温ソフト化の特徴的な実験事実を下記に箇条書きし，オフセンターラットリングとは何かを浮き彫りにしよう.¥¥

【低温ソフト化】

1. キュリー・ワイス則に従う低温ソフト化が観測される．解析により得られるワイス温度は負で
2. La系では$T$ = 20 mKにおいても，低温ソフト化が止まらない.
3. LaOs$_4$Sb$_{12}$はBCS 超伝導転移を迎えても低温ソフト化が続くが，PrOs$_4$Sb$_{12}$の低温ソフト化は非BCS超伝導転移温度で止まる.
   
   【超音波分散】
   
   
4. アレニウス型の緩和時間の温度依存性で良く説明できる.
5. 低キャリアのCeOs$_4$Sb$_{12}$では観測されていない．
   
   【低温ソフト化と超音波分散に共通する特徴】
   
   
6. $4f$ 電子を持たないLa化合物でも観測され，磁場の影響を全く受けない
7. 超音波分散無き物質では低温ソフト化は観測されていない．
8. $Ln$Os$_4$Sb$_{12}$, $Ln$$_3$Pd$_{20}$Ge$_6$では明瞭な超音波モード依存性がある（一方で$Ln$Fe$_4$Sb$_{12}$では$C_{11}$, $C_{44}$モードの両方で超音波分散が観測され，モード依存性は無い）.
   

これらの現象の解釈には論争中で未解明なものも混ざっている．先ず，確実に言えることから述べよう．
上記の実験事実1.)と6.)から，低温ソフト化の起源は$4f$電子の四極子自由度とは異なる電荷自由度による局所的且つインコヒーレントな現象であり，サイト間相互作用が反強的であることがわかる．そして実験事実 2.)から，その量子状態は20 mKに於いても縮退を保ち続けていると言える．一方，実験事実 4.)から『超音波分散の起源は熱活性型の緩和現象である』ことがわかる．また，6.)のような共通の性質を持つことから，少なくとも低温ソフト化と超音波分散の起源が非磁性で，歪み場と結合する局所電荷自由度であることは結論できる．

これ以降は，未解明の部分である.
　まず実験事実 5.)は，超音波分散が単にカゴの中にイオンを閉じこめ，カゴのサイズを大きくすれば実現するような単純な起源ではないことを示唆する．非弾性中性子散乱実験や，ラマン散乱では数meVのエネルギーを持つゲストモードがCeRu$_2$Sb$_{12}$やCeOs$_4$Sb$_{12}$において共通して観測されているのに対し，どちらの系でも超音波分散は観測されない．一方，充填スクッテルダイト化合物のCe系化合物はほとんどが低温で強い混成効果による低キャリアの近藤絶縁体，もしくは近藤半導体となる．そのため，内包イオンの局所振動が格子系と結合し，超音波分散として現れるためには伝導電子との相互作用が必要なのではないかという推測に達する．服部らは$¥Gamma$点近傍の音響フォノンと光学フォノン間の波数に依存する混成を考え，伝導電子と光学フォノンの結合によるエネルギー散逸機構により，音響フォノンが変調を受け，超音波測定はそれを超音波分散として捉えたものであるという理論提案を行っている. [76]

また一方で，伝導電子が居る系においても，実験事実 8)が示すように，カゴを構成する一部の元素の置換によって超音波分散が全く観測されないというコントラストがあらわれている[51,65]．具体的に書くと，$Ln$Os$_4$Sb$_{12}$, $Ln$Fe$_4$Sb$_{12}$で低温ソフト化と超音波分散は観測されるが，$Ln$Ru$_4$Sb$_{12}$では観測されない[72]．同様に，$Ln$$_3$Pd$_{20}$Ge$_6$では観測されるが，$Ln$$_3$Pd$_{20}$Si$_6$では観測されていない．これらの場合，元素の置換によってカゴの大きさも変化するため，超音波分散の活性エネルギーが変化し，問題は単純ではない．即ち，共鳴条件$¥omega ¥tau ¥sim 1$を満たす超音波の測定周波数と温度が測定可能な実験条件に入らない場合，超音波では観測できないことになるからである．超音波分散と低温ソフト化の起源が共通の根を持つのかどうかはまだはっきりしていないが，低温ソフト化が観測される系では必ず高温側に超音波分散が観測されているという実験事実 7)は，両者に何らかの関係があることを示唆する．石井らは，La$T_4$Sb$_{12}$ ($T$ = Fe, Ru, Os)において，遷移金属Os, Ru, Feの持つ伝導バンドのフェルミ面上での状態密度がFe $>$ Os $>$ Ruの順に大きいことと，超音波分散・低温ソフト化の発現に相関があることを指摘している[66]．もしそうならば8)に示した超音波分散が現れるかどうかのコントラストとモード依存性は，フォノンと伝導電子との結合の大小や異方性により生じていることになるだろう．一方，超音波分散が観測される充填スクッテルダイト化合物において$^{139}$La-NMRの超微細結合定数が負の値を示すことが指摘されており[67]，5.2章の最後に述べた「核四極子」と歪みとの関係を臭わせる．

さて，LaFe$_4$Sb$_{12}$はnon-$4f$系にしては比較的高い電子比熱係数$¥gamma$の存在が興味深い[68]．そのため電荷揺らぎの自由度とフォノンや伝導電子が強結合系を生み出るというエキゾチックな重い電子状態の形成機構が議論されている．次章ではその典型例であるSmOs$_4$Sb$_{12}$の超音波分散の観測について紹介しよう．

図32 LaOs$_4$Sb$_{12}$の弾性定数$C_{11}$の超音波分散 (a) 周波数依存性の実験結果, (b)計算, (c)超音波吸収係数[64]

図33 PrOs$_4$Sb$_{12}$の弾性定数$C_{11}$の超音波分散 (a) 周波数依存性の実験結果, (b)計算, (c)超音波吸収係数

図34 NdOs$_4$Sb$_{12}$の弾性定数$C_{11}$の超音波分散 (a) 周波数依存性の実験結果, (b)計算, (c)超音波吸収係数 [75]

図35 LaOs$_4$Sb$_{12}$の弾性定数$C_{11}$の低温ソフト化[60]

(第6章に続く）