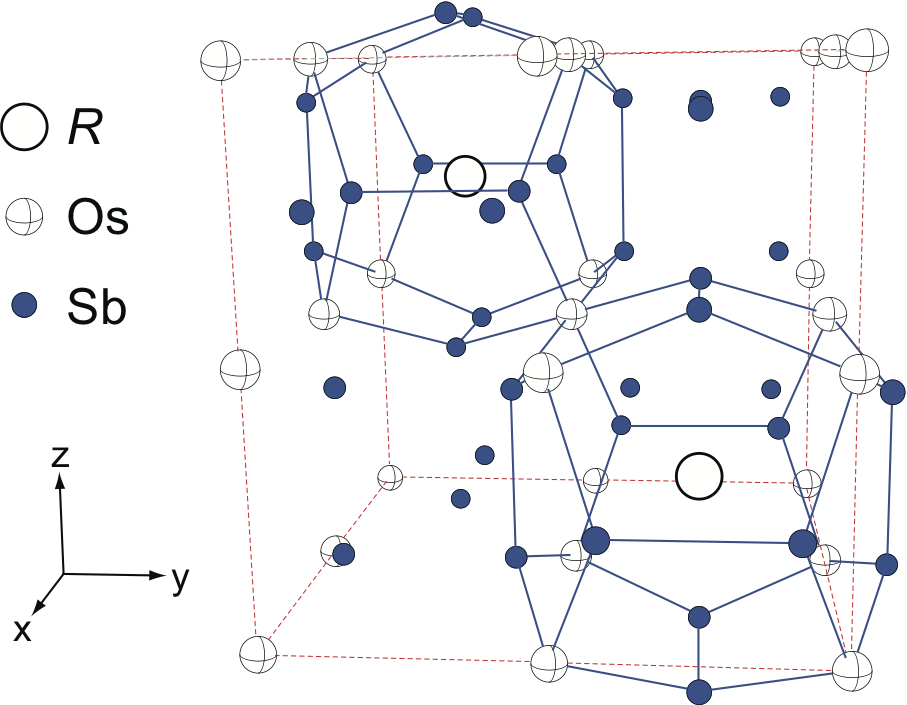
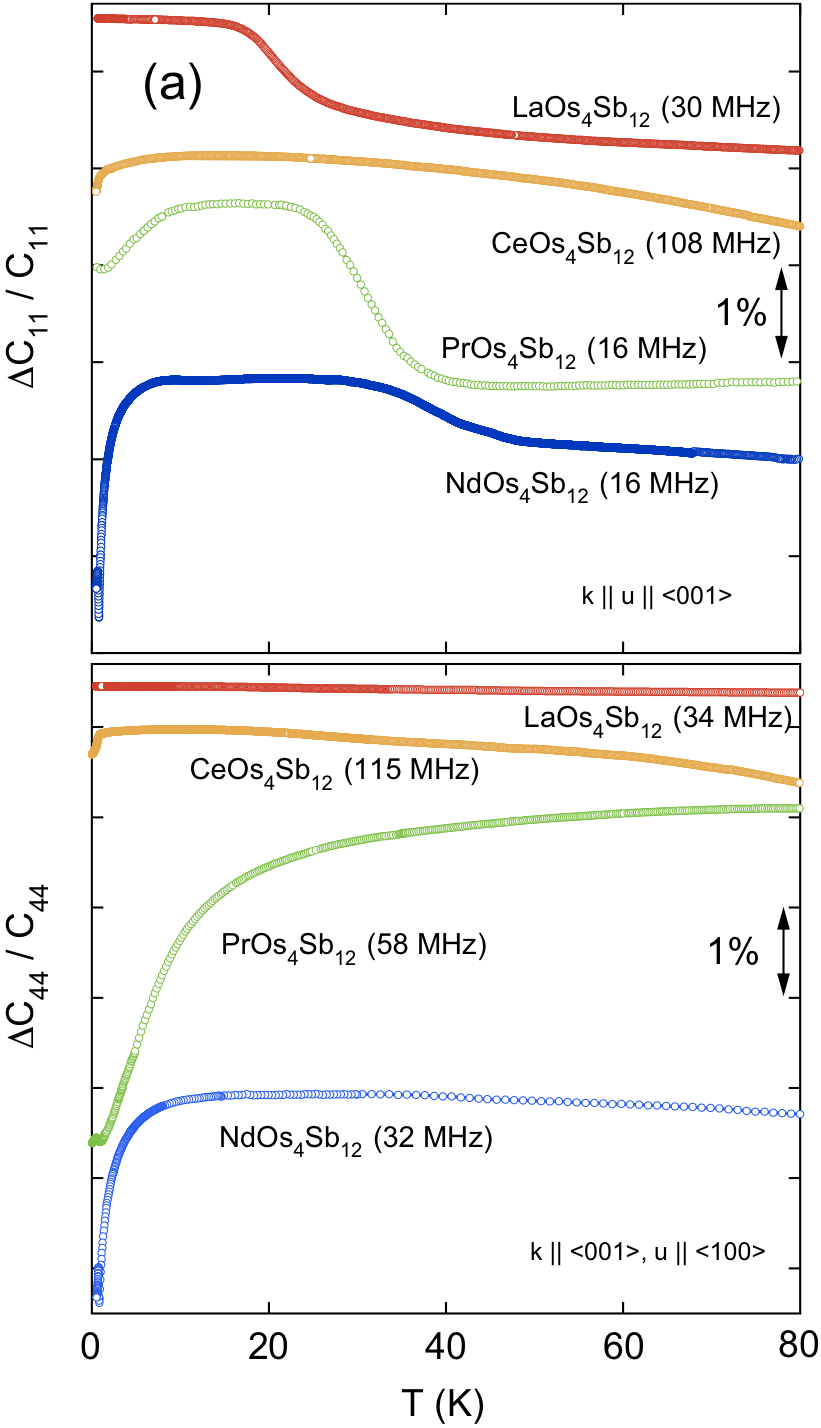
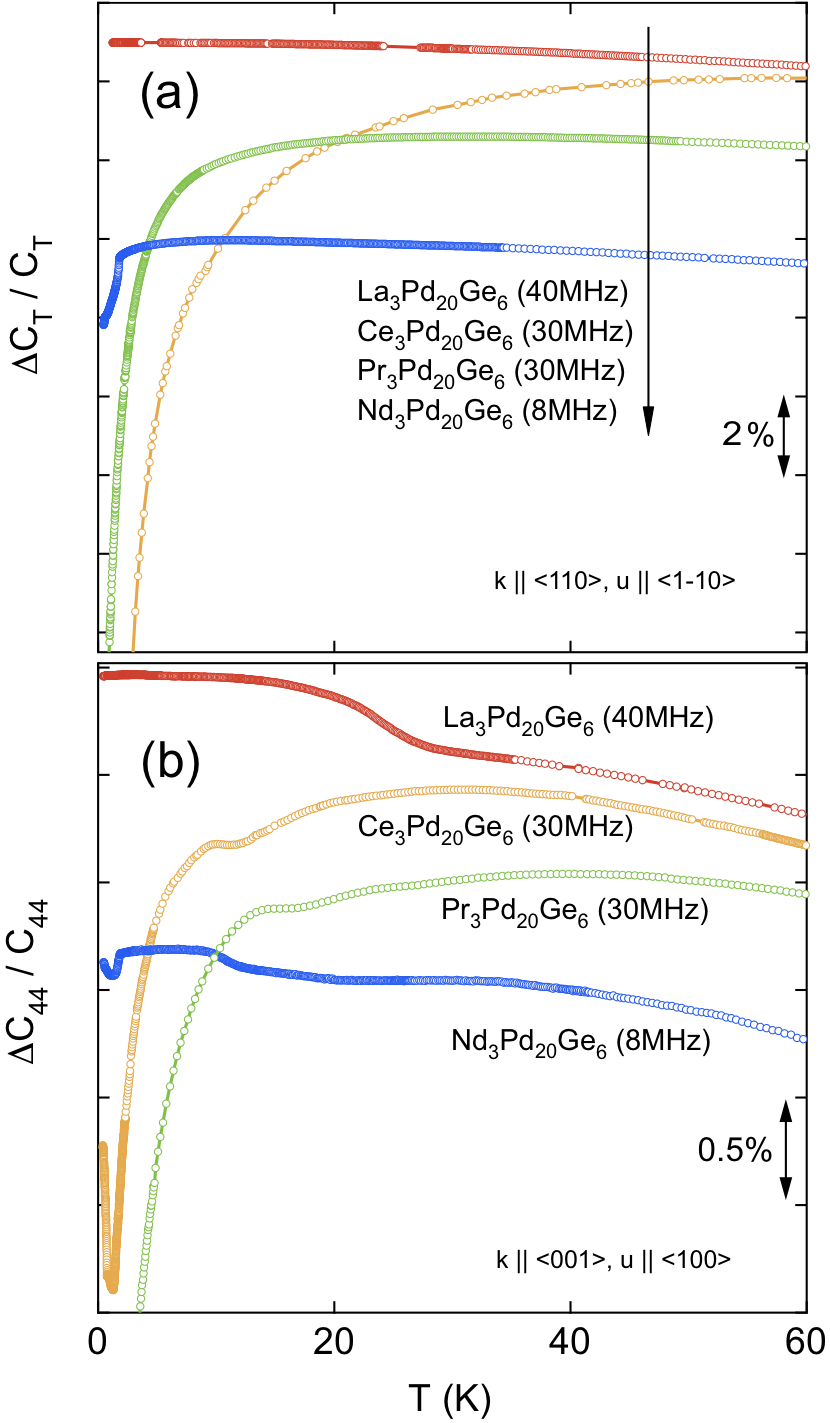
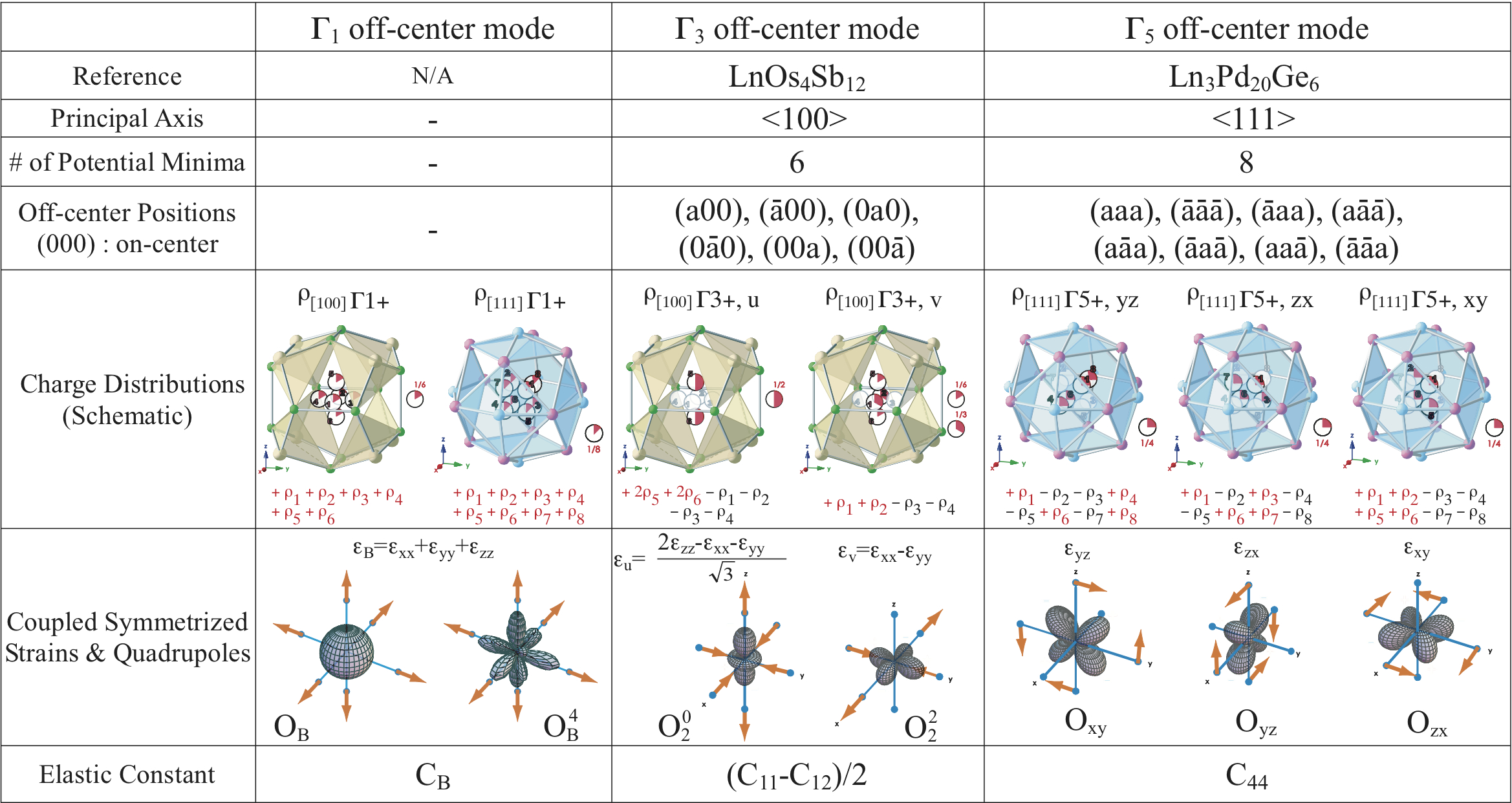
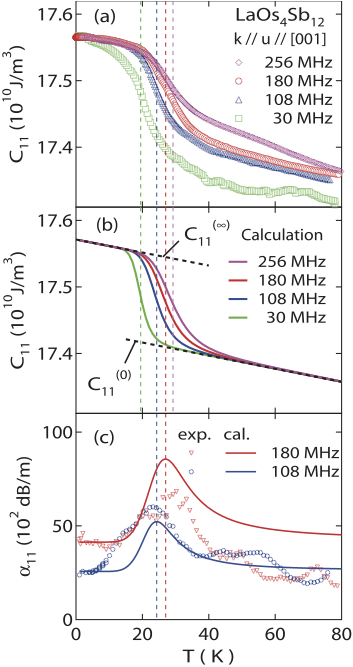
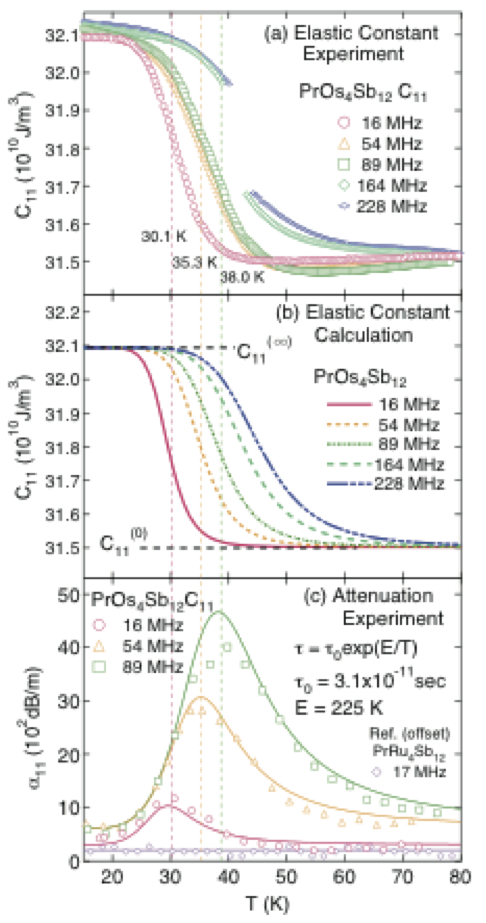
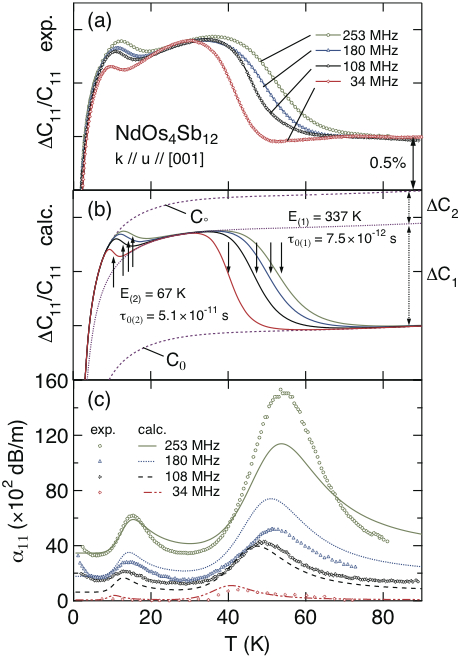
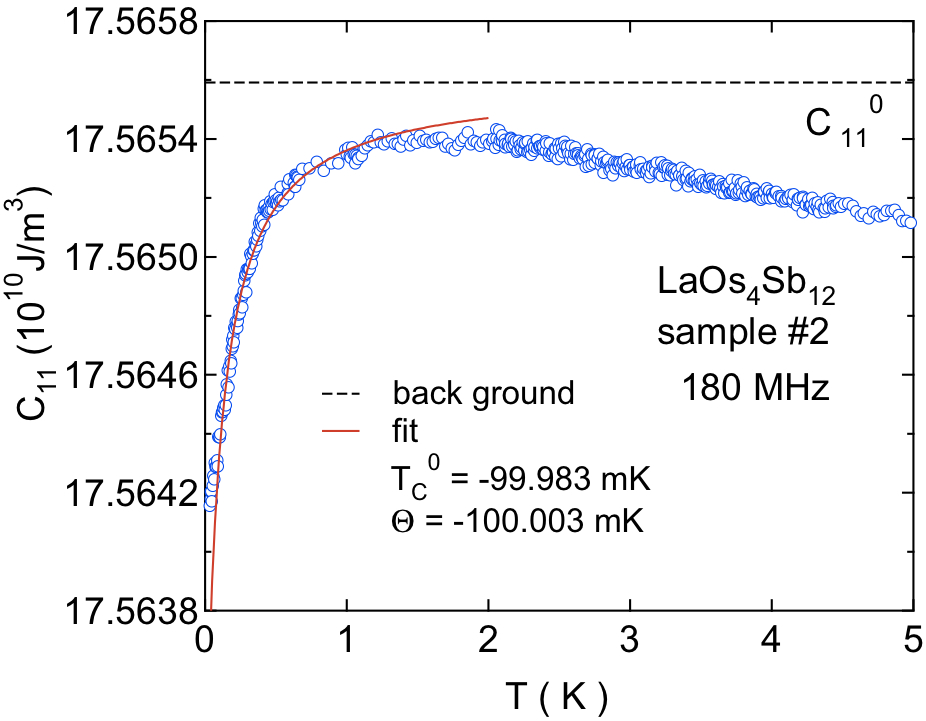
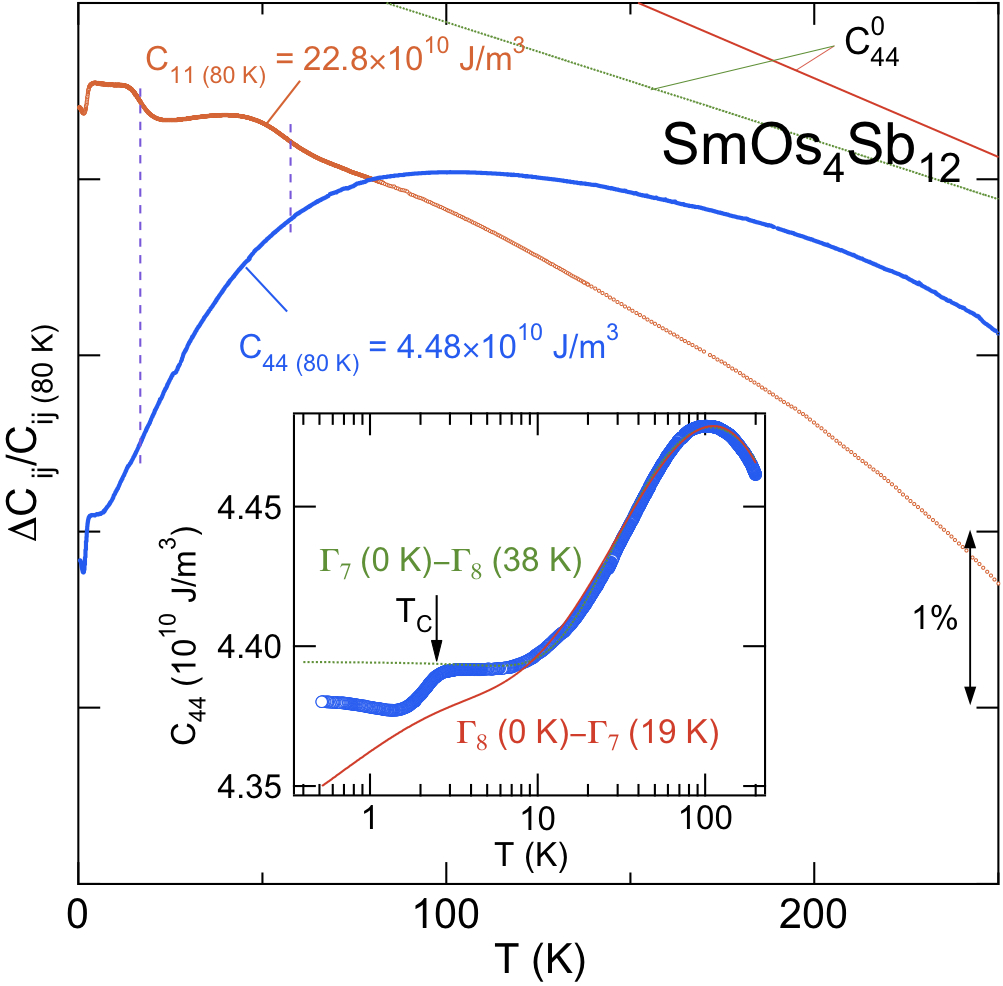
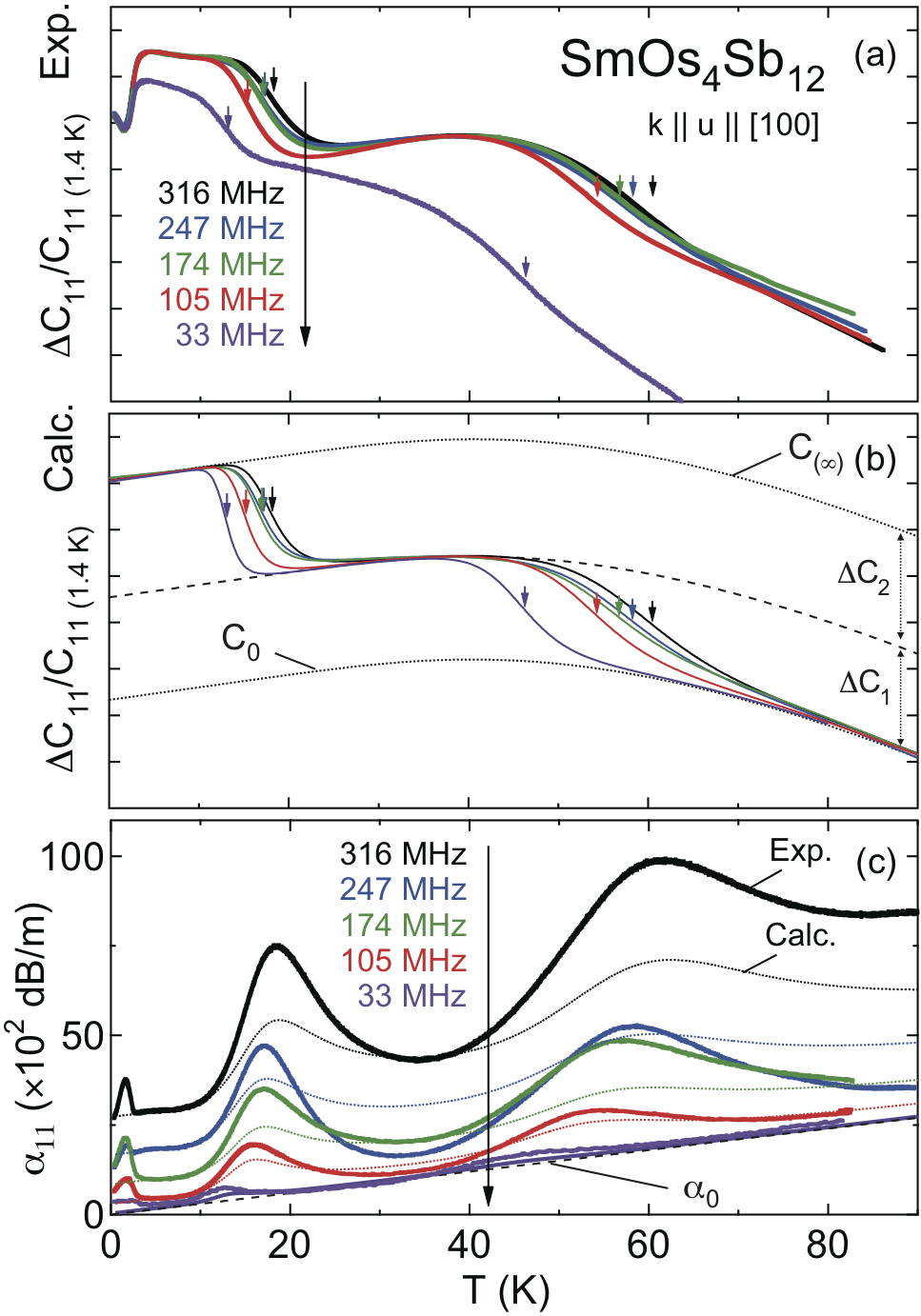
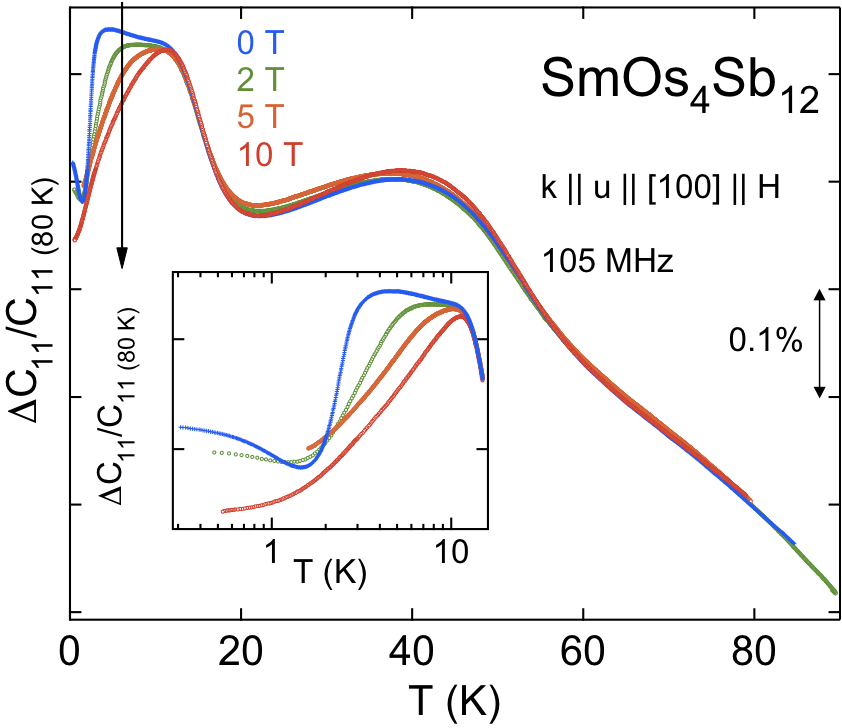
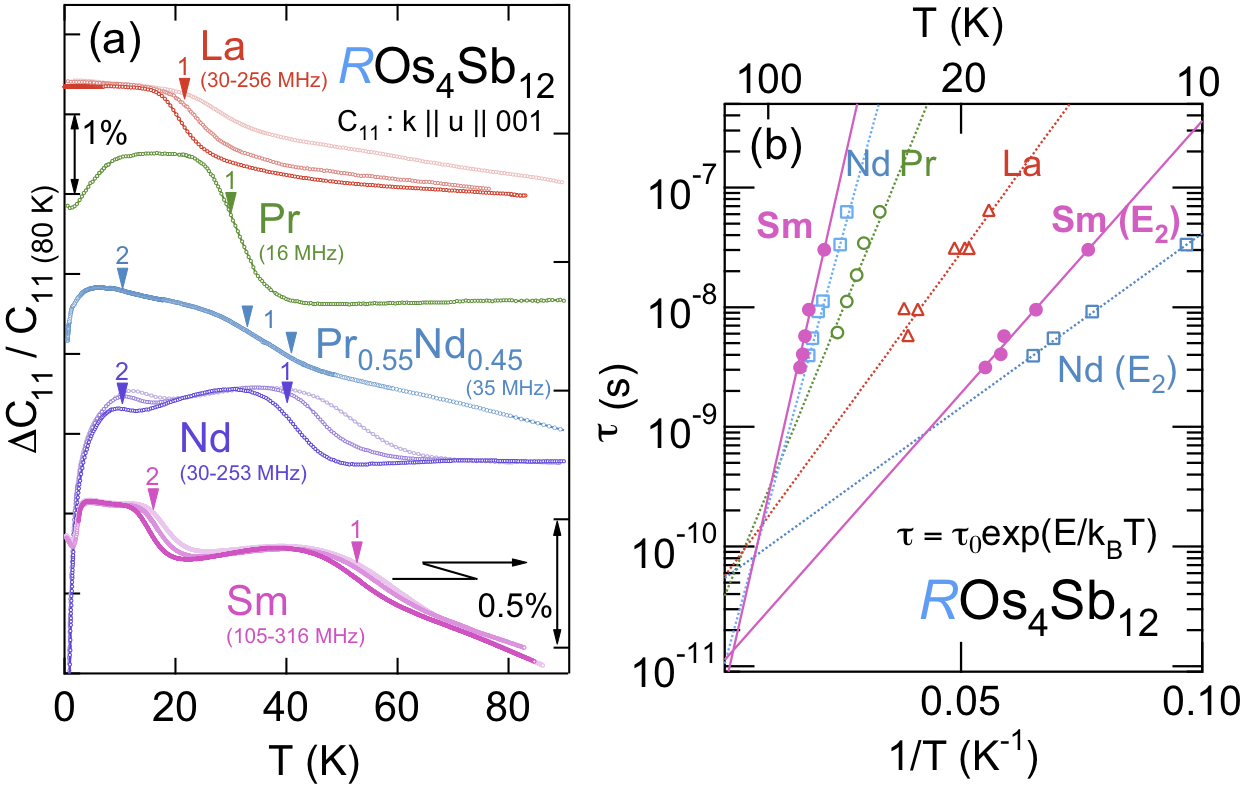
本稿は、
新学術領域研究(研究領域提案型)「重い電子系の形成と秩序化」が主催した「重い電子系若手秋の学校’11」のテキストブックをHTML化したものです。
おわりに
超音波で観測される弾性定数の温度(周波数)依存性を,四極子感受率,緩和の現象論を用いて解釈する方法を述べてきた.本稿では詳細に立ち入らなかったが,歪み場は磁場と直交するため,磁場中での超音波測定は多極子やオフセンター自由度を分光学的に調べる上で強力なプローブとなる.また,一軸圧力下,静水圧力下などの多重極限環境下における超音波測定の手法も確立しつつあり,今後ますますその重要性が認識されていくことと思う.重い電子系においては一般的に遍歴性が強く,局在四極子モーメントが遮蔽されることで感受率として理解することが難しくなる場合があるが,他方,多チャンネル近藤効果や上述のオフセンター自由度に由来するエキゾチックな多体効果が期待される系では,四極子と結合する超音波測定の切り口から量子基底状態を明らかにすることが求められるだろう.
日本における超音波電子物性研究は現新潟大学教授の後藤輝孝先生が今から約40年前にフランクフルト大学のBruno Lüthi先生のもとで習得した技術を東北大学の旧科学技術計測研究所で発展させたことが始まりである.実は,超音波測定はNMRとほぼ同じ発振器,検波器の構成で測定できる. 昨今の携帯電話等の普及によって比較的安価に高周波装置が手に入るようになったこともあり,もはや誰にでも簡単に測定系を構築できる非常に汎用性の高い手法となった.X線装置やMPMSのように一機関に一台ずつとは言わないが,少なくとも単結晶の基礎物性評価を行っているグループに於いては,もっと普及して然るべきだと著者は個人的に考える.本稿を読んだ学生諸君が少しでも超音波物理に興味を持ち,ご自身の研究テーマに応用する可能性を考えていただけたならば何よりの幸いである.近い将来,日本語の超音波物性の教科書が出版される筈であるが,それまでの間,初心者にとっては下記の参考文献の中でも特に番号の後に*を付けたものから当たってみるのが超音波測定のデータを読み解くための近道であると思う.著者の能力不足で本稿には不十分な点が多々あると思うが,どうかご容赦いただきたい.
謝辞
重い電子若手秋の学校の実行委員の皆様には,本稿を執筆する機会を与えていただき感謝申し上げます.本稿の執筆にあたり,以下の方々(敬称略)からご協力をいただきました.ここに感謝申し上げます.
鈴木孝至(広島大学),石井勲(広島大学),藤秀樹(神戸大学),馬場正太郎(新潟大学),荒木幸治(新潟大学 / HLD),赤津光洋(新潟大学),日高宏之(北海道大学 / CPBF),門別翔太(北海道大学).
本稿で紹介した研究成果の一部は,下記の研究グラントによる援助を受けたものです.
- 文部科学省科学技術研究費補助金
- 新学術領域研究「重い電子の形成と秩序化」公募研究 (No. 21102501)
- 特別推進研究「電荷揺らぎに由来する強相関量子相の研究」(No. 18002008)
- U.S. Department of Energy Grant No. DE-FG02-04ER46105
- U.S. National Science Foundation Grant No. DMR 0802478
- CCSA Grant No. 7669. (P.-C. Ho)
- 北海道大学基礎科学融合領域リーダ育成システム
参考文献
[01] T. Goto et al. , J. Phys. Soc. Jpn. 75 (2006) 044602.
[02] 後藤輝孝, 超音波便覧 pp. 281 (丸善 1999)
[03] *後藤輝孝, 根本祐一 日本物理学会誌 61 (2006) 408.
[04] S. Baba et al. , J. Phys. Soc. Jpn. 80 (2011) 094601.
[05] B. Wolf et al. , Physica B 294&295 (2001) 612.
[06] *B. Lüthi, Physical Acoustics in the Solid State (Springer Berlin Heidelberg New York 2005).
[07] K. R. Lea, M. J. M. Leask, and W. P. Wolf, J. Phys. Chem. Solids 23 (1962) 1381.
[08] T. Tayama et al. , J. Phys. Soc. Jpn. 70 (2001) 248.
[09] M. Niksch et al. , Helvetica Phys. Acta 55 (1982) 688.
[10] M. Kasaya et al. , Physica B 281&282 (2000) 579-580.
[11] R. M. Galera et al. , J. Magn. Magn. Mater. 23 (1981) 317.
[12] T. M. Kelley et al. , Phys. Rev. B 61 (2000) 1831.
[13] O. Suzuki et al. , J. Phys. Soc. Jpn. 75 (2006) 013704.
[14] T. Onimaru et al. , J. Phys. Soc. Jpn. 106 (2011) 177001.
[15] K. Araki et al. , Phys. Rev. B 84, 045110 (2011).
[16] K. Takegahara et al. , J. Phys. Soc. Jpn. 70 (2001) 1190.
[17] T. Yanagisawa et al. , Phys. Rev. B 77 (2008) 094435.
[18] S. Nakamura et al. , J. Phys. Soc. Jpn. 63 (1994) 623.
[19] E. D. Bauer et al. , Phys. Rev. B 65 (2002) 100506(R).
[20] T. Goto et al. , Physica B 359-361 (2005) 822&826.
[21] *根本祐一 スクッテルダイト若手夏の学校 テキスト 2006年8月7日-10日 於 飛騨高山 (文部科学省 科学研究費補助金 特定領域研究「充填スクッテルダイト構造に創出する新しい量子多電子状態の展開」主催.
[22] M. B. Maple et al. , Journal of Superconductivity and Novel Magnetism 19 (2006) 3.
[23] 酒井治, 重い電子系の形成と秩序化ニュースレター Vol.3 No.2 (2011) pp. 5.
[24] T. Fujita et al. , Solid State Commun. 35 (1980) 569.
[25] H. Yamauchi et al. , J. Phys. Soc. Jpn. 65 (1999) 2057.
[26] K. Hirota et al. , Phys. Rev. Lett. 84 (2000) 2706.
[27] H. Yamauchi et al. , J. Phys. Soc. Jpn. 71 (2002) 94.
[28] Y. Nemoto et al. , Physica B 329-333 (2003) 641-642.
[29] T. Yamaguchi et al. , Physica B 329-333 (2003) 622-623.
[30] A. Dönni et al. , J. Phys. Soc. Jpn. 70 (2001) A 448-450.
[31] O. Suzuki et al. , J. Phys. Soc. Jpn. 67 (1998) 4243.
[32] T. Tayama et al. , J. Phys. Soc. Jpn. 66 (1997) 2268.
[33] O. Suzuki et al. , J. Phys. Soc. Jpn. 74 (2005) 735.
[34] M. Akatsu et al. , J. Phys. Soc. Jpn. 72 (2003) 205-208.
[35] K. Kubo and Y. Kuramoto, J. Phys. Soc. Jpn. 72 (2003) 1859.
[36] K. Kubo and Y. Kuramoto, J. Phys. Soc. Jpn. 73 (2004) 216.
[37] D. Mannix et al. , Phys. Rev. Lett. 95 (2005) 117206.
[38] K. Kuwahara et al. , J. Phys. Soc. Jpn. 76 (2007) 093702.
[39] 柳澤達也, 新潟大学博士論文 (2003).
[40] D. L. Cox and A. Zawadowski, Adv. Phys. 47 (1998) 599.
[41] Y. P. Varshny, Phys. Rev. B 2 (1970) 3952.
[42] B. Lüthi et al. , J. Low. Temp. Phys. 95 (1994) 257.
[43] T. Suzuki et al. , J. Phys. Soc. Jpn. 54 (1985) 27.
[44] D. Weber et al. , Europhys. Lett. 3 (1987) 827.
[45] S. Raymond et al,, Solid State Commun. 118 (1993) 454.
[46] B. Wolf et al. , J. Low Temp. Phys. 94 (1994) 307.
[47] M. Yoshizawa et al. , J. Magn. Magn. Matt. 52 (1985) 413.
[48] W. Gebhardt and U. Krey, Phase transition and critical phenomena , Vieweg¥&Sohn, Braunschweig/Wiesbaden (1980).
[49] D. Weber, Doctoral thesis, Johann Wolfgang Goethe Univ., Frankfurt (1991).
[50] D. J. Braun and W. Jeitschko, J. Less Common Met. 72 (1980) 147.
[51] M. Udagawa et al. , J. Phys. Soc. Jpn. 77 (2008) A 142-147.
[52] N. Ogita et al. , Physica B 383 (2006) 128.
[53] S. Tsutsui et al. , J. Phys. Soc. Jpn. 77 (2008) Suppl. A 257.
[54] K. Iwasa et al. , J. Phys. Conf. Ser. 92 012122.
[55] V. Keppens et al. , Nature 395 (1998) 876.
[56] T. Goto et al. , Phys. Rev. B 70 (2004) 184126.
[57] Y. Nemoto et al. , Phys. Rev. B 68 (2003) 184109.
[58] T. Goto et al. , Phys. Rev. B 69 (2004) 180511(R).
[59] T. Yamaguchi et al. , Physica B 359-361 (2005) 296-298.
[60] T. Goto et al. , Phys. Rev. B 59 (1999) 269.
[61] E. Kanda et al. , J. Phys. Soc. Jpn. 54 (1985) 175.
[62] R. P. Devaty and A. J. Sievers, Phys. Rev. B 19 (1979) 2343.
[63] K. Kaneko et al. , J. Phys. Soc. Jpn. 78 (2009) 074710.
[64] Y. Yasumoto et al. , J. Phys. Soc. Jpn. 77 (2008) Suppl. A 242.
[65] C. H. Lee et al. , J. Phys. Soc. Jpn. 75 (2006) 123602.
[66] I. Ishii et al. , J. Phys. Soc. Jpn. 78 (2009) 084601.
[67] Y. Nakai et al. , Phys. Rev. B 77 (2008) 041101.
[68] K. Matsuhira et al. , J. Phys. Soc. Jpn. 78 (2009) 124601.
[69] W. M. Yuhasz et al. , Phys. Rev. B 71 (2005) 104402.
[70] S. Sanada et al. , J. Phys. Soc. Jpn. 74 (2005) 246.
[71] M. Mizumaki et al. , J. Phys. Soc. Jpn. 76 (2007) 053706.
[72] Y. Nemoto et al. , J. Phys. Soc. Jpn. 77 (2008) Suppl. A 153.
[73] Y. Nakanishi et al. , J. Phys.: Conf. Ser. 51 (2006) 251.
[74] T. Yanagisawa et al. , J. Phys. Soc. Jpn. 80 (2011) 043601.
[75] T. Yanagisawa et al. , J. Phys. Soc. Jpn. 77 (2008) 074607.
[76] K. Hattori et al. , J. Phys. Soc. Jpn. 74 (2005) 3306.
[77] C. C. Yu and P. W. Anderson, Phys. Rev. B 29 (1984) 6165.
[78] H. Kotegawa et al. , J. Phys. Soc. Jpn. 77 (2007) Suppl. A 90.
(もくじに戻る)