第6章　磁場に鈍感な重い電子系

SmOs₄Sb₁₂の弾性応答

SmOs$_4$Sb$_{12}$は充填スクッテルダイト化合物であり，比較的大きな電子比熱係数$¥gamma$ = 820 [mJ mol$^{-1}$ K$^{-2}$]が比熱から見積もられている[70,71]．驚くべき事に，$H ¥| ¥langle 001 ¥rangle$ 方向の32 [T]の強磁場下に於いても電子比熱係数が減少せず，ほぼ一定値を保つことから，CeやYb化合物で観られる従来型の磁気近藤効果とは異なる, 非磁性起源の重い準粒子有効質量の形成機構が提案されている．また，本系は$T_{¥rm C} =$ 2.5 [K]で非常に弱い強磁性モーメント($M_s ¥sim 0.087¥mu_B$)を伴う何らかの秩序を起こし，そこで放出されるエントロピー$R¥ln2$の1.6 ¥%と多体効果による遮蔽が大きい．結晶場基底状態は，ショットキー比熱の解析と，磁化過程の磁場方向異方性の解析から，それぞれ$¥Gamma_7$と$¥Gamma_8$基底状態のモデルが提案されているが，決着はついていない．Smは価数揺動し易いイオンである．共鳴X線散乱実験によりSmイオンの価数の温度依存性が調べられており，$T ¥sim$ 150 Kから25 KにかけてSmの平均価数は2.83から2.76の間を単調に変化することが報告されている[71]．
本系におけるゲストイオンの局所振動の傍証として，これまでにラマン散乱による，LnOs$_4$Sb$_{12}$の系統的な測定によりゲスト原子由来のラマンモードが数十cm$^{-1}$に存在することが確認されており，$^{123}$Sb-NQRでは$1/T_2$に20－30 K付近に数ms$^{-1}$のピーク等が観測されている[51,78]．これらは超音波分散が観測されている$Ln$ = La, Pr, Ndでも同様に観測されることから[72]，本系においても超音波分散の観測が期待されていた[73]．そこで，我々はSb自己フラックス法により0.75×0.75×0.50 mm$^3$程度の大きさの単結晶試料を育成し，超音波測定を行った[74]．

6.1 結晶場効果

図36にSmOs$_4$Sb$_{12}$の弾性定数$C_{11}$と$C_{44}$の温度依存性を示す．縦波弾性定数$C_{11}$は室温から単調に増加し，図の縦点線の温度で２段のショルダー型の弾性異常を示す．この弾性異常は超音波吸収を伴い，その周波数依存性が熱活性型であることから$R$ = La, Pr, Ndで観測されたものと同様の超音波分散であると考えられる．本系でも横波弾性定数$C_{44}$には超音波分散が観測されないことが確かめられている．その弾性定数$C_{44}$は100 K付近から結晶場効果に由来する「ソフト化」を示し，10 K付近で徐々に一定値に収束する．$T_{¥rm C}$ = 2.5 Kにおいて両方の弾性定数にステップ状のとびが観測されるが，この弾性異常は相転移に起因するもので，CeCu$_6$やCeRu$_2$Si$_2$で縦波超音波にあらわれたような近藤一重項形成による「ソフト化」とは異なる．

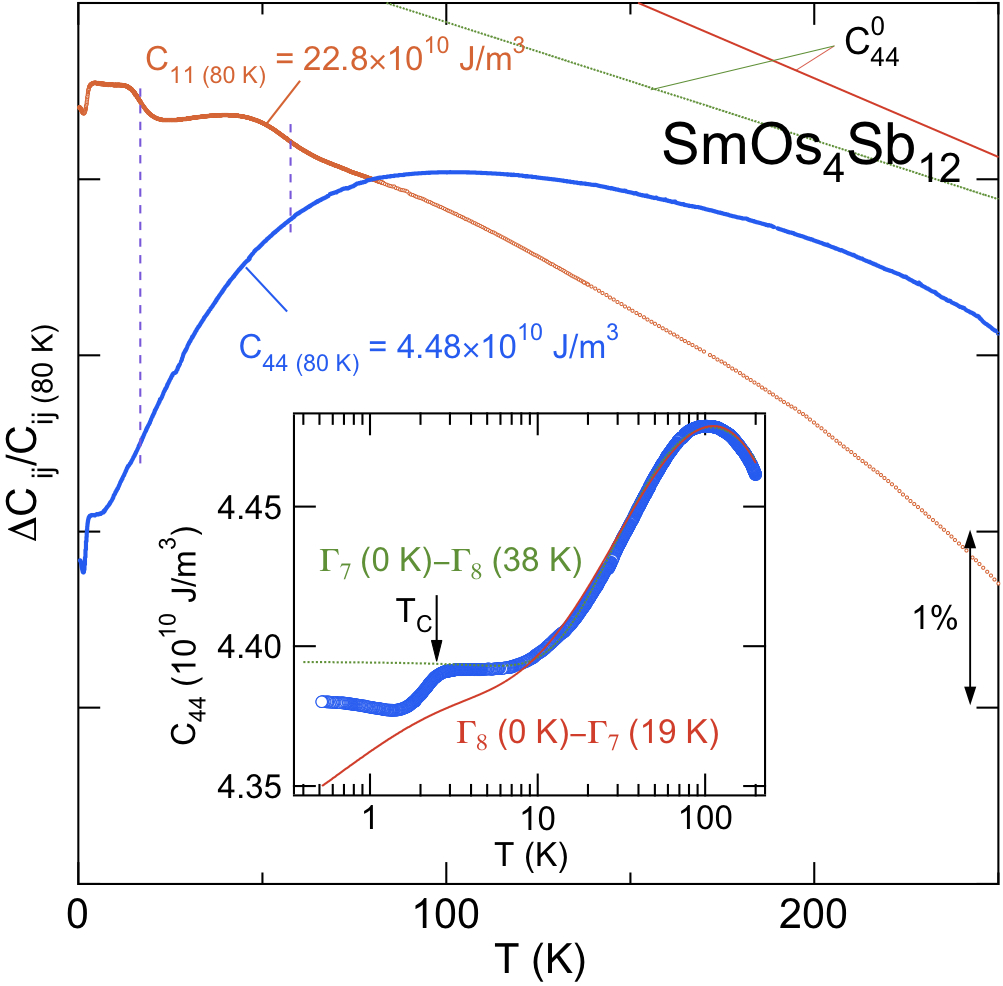
図36 SmOs$_4$Sb$_{12}$の弾性定数$C_{11}$, $C_{44}$の温度変化.

図36内挿図は過去に提案されている$¥Gamma_7$基底と$¥Gamma_8$基底の二つの結晶場レベルスキームに基づいた四極子感受率による解析結果で，横軸は温度を対数表示している．$¥Gamma_7$基底モデル（$¥Gamma_7$(0 Κ)-$¥Gamma_8$(38 Κ)）は$T_C$までの温度依存性を良く説明し，$¥Gamma_8$基底モデル（$¥Gamma_8$(0 Κ)-$¥Gamma_7$(19 Κ)）では10 K付近で実験値からずれる結果が得られた．それぞれの解析で得られたパラメータは，$¥Gamma_7$基底の場合，四極子格子結合定数が$|g| = 258$ K，四極子間相互作用の結合定数が $g′= －0.79$ K，$¥Gamma_8$基底の場合$|g| = 369$ K と $g′= －1.76$ Kである．ここで注意すべきは，本系では多体効果が10 K付近から効いていると考えられるので，多体効果によって結晶場効果による「ソフト化」が抑えられる可能性がある．3.4章で紹介したCXcal-excelの計算はCe$^{3+}$の場合の近藤効果について特化された計算結果であるため，同じ全角運動量$J = 5/2$を持つとはいえども性質の異なるSm$^{3+}$の実験値との定量的な比較は出来ない．しかし，大まかな傾向を知る事はできる．図11と図12によれば，$¥Gamma_8$基底の場合でも10 K程度の近藤温度を仮定すれば$¥Gamma_7$基底と同様に, 低温で一定値に収束する弾性定数$C_{44}$の温度依存性を再現できるため，$¥Gamma_8$基底の可能性は依然として残る．

尚，上記の議論に於いては価数揺動の効果は考慮していない．Sm$^{2+}$ ($J = 0$)は四極子自由度を持たないため，その状態が混ざったとしても，四極子感受率の強度に体積分率程度のファクターがかかるものの，実験結果の解析にはさほど影響を与えないと考えられるからである．弾性定数$C_{44}$は10 Kまで2¥%程度のソフト化を示しているので，超音波実験からは，少なくとも10 K以上の領域ではSmの$4f$ 電子状態は局在性が強く，弾性定数の温度依存性はSm$^{3+}$の１イオン感受率で説明できていると言える。

6.2 超音波分散

さて，次に$C_{11}$の超音波分散を詳しくみていこう。図37に弾性定数$C_{11}(¥omega)$超音波吸収係数$¥alpha_{11}(¥omega)$の周波数依存性を示す。図37(b)と(c)に実線で示したのは現象論による解析であり，実験結果をよく再現している。図38に105 MHzで測定した弾性定数$C_{11}$の磁場依存性を示した。結晶場のゼーマン分裂により結晶場効果によるソフト化が10 K以下で徐々に現れるが，２つの超音波分散に伴うショルダー型の弾性異常は磁場に影響を受けていないことが解る。このことは(何度も繰り返すが), 二つの超音波分散が非磁性起源であることを裏付けている。

SmOs$_4$Sb$_{12}$では，低温秩序による弾性異常と結晶場によるソフト化が現れるため，LaOs$_4$Sb$_{12}$で現れた様なオフセンター自由度に由来する「低温ソフト化」が共存しているかどうかは確認できていない．正確な結晶場レベルスキームを決定し，極低温・高磁場下において結晶場効果とオフセンター自由度を分離する実験を現在試みている．

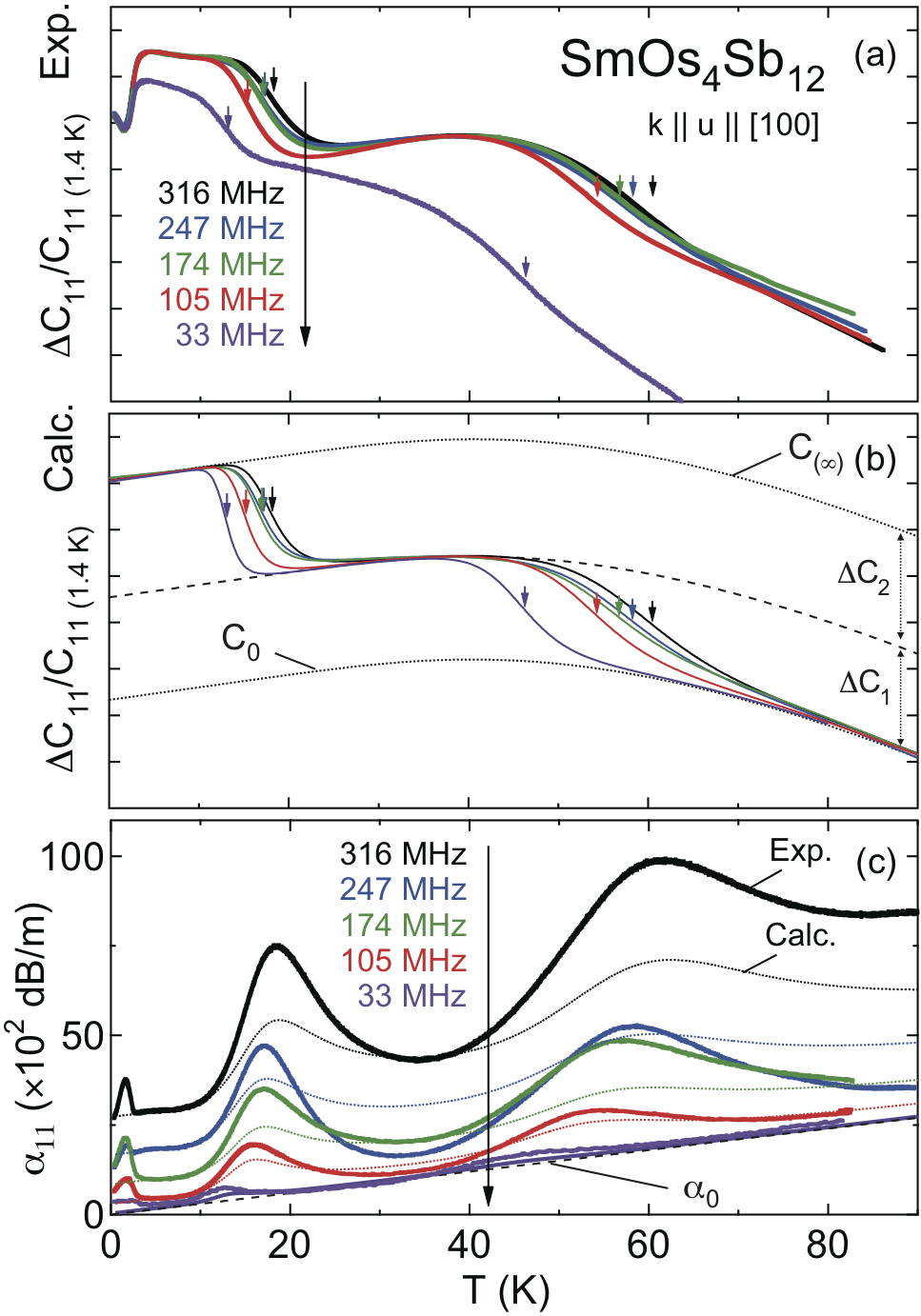
図37 SmOs$_4$Sb$_{12}$の弾性定数$C_{11}$の超音波分散 (a) 周波数依存性の実験結果, (b)計算, (c)超音波吸収係数

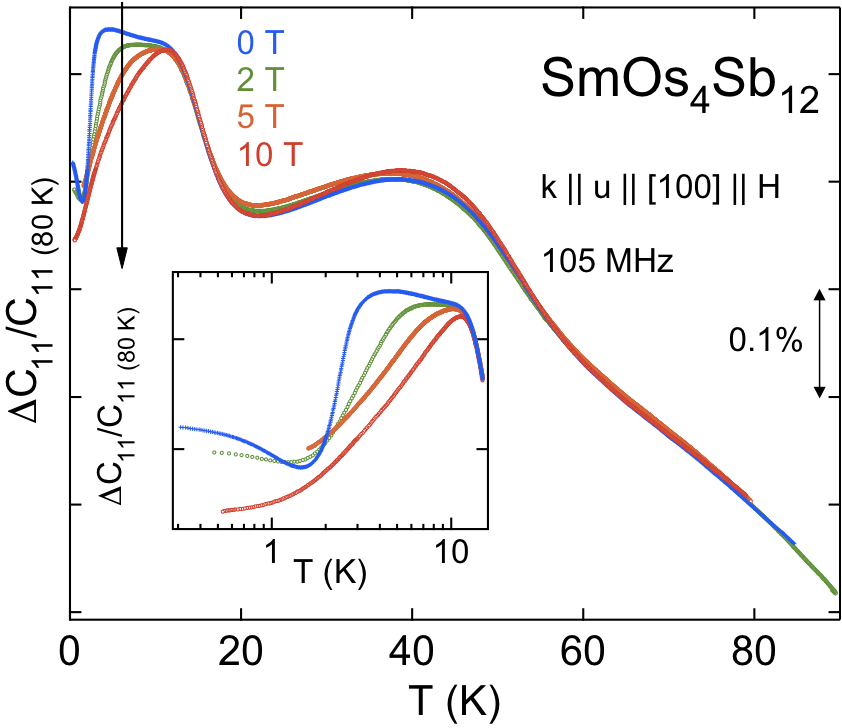
図38 SmOs$_4$Sb$_{12}$の弾性定数$C_{11}$の温度変化磁場依存性

6.3 熱活性エネルギーと他の物理量の比較

図39(a)に$Ln$Os$_4$Sb$_{12}$の弾性定数$C_{11}$に現れる超音波分散の系統変化を示し，図39(b)には$Ln$Os$_4$Sb$_{12}$の超音波分散の解析で得られた活性エネルギー$E$と特性時間$¥tau_0$をアレニウスプロットによって比較した．回帰直線の傾きが活性エネルギーに対応し，マーカーは共鳴条件$¥omega ¥tau ¥sim 1$を満たす温度に対応する．表6にそれらのパラメータと併せてデバイ温度，アインシュタイン温度，電子比熱係数等を，超音波分散が観測されている類似物質の$Ln$Fe$_4$Sb$_{12}$の諸値と共に比較表示した．

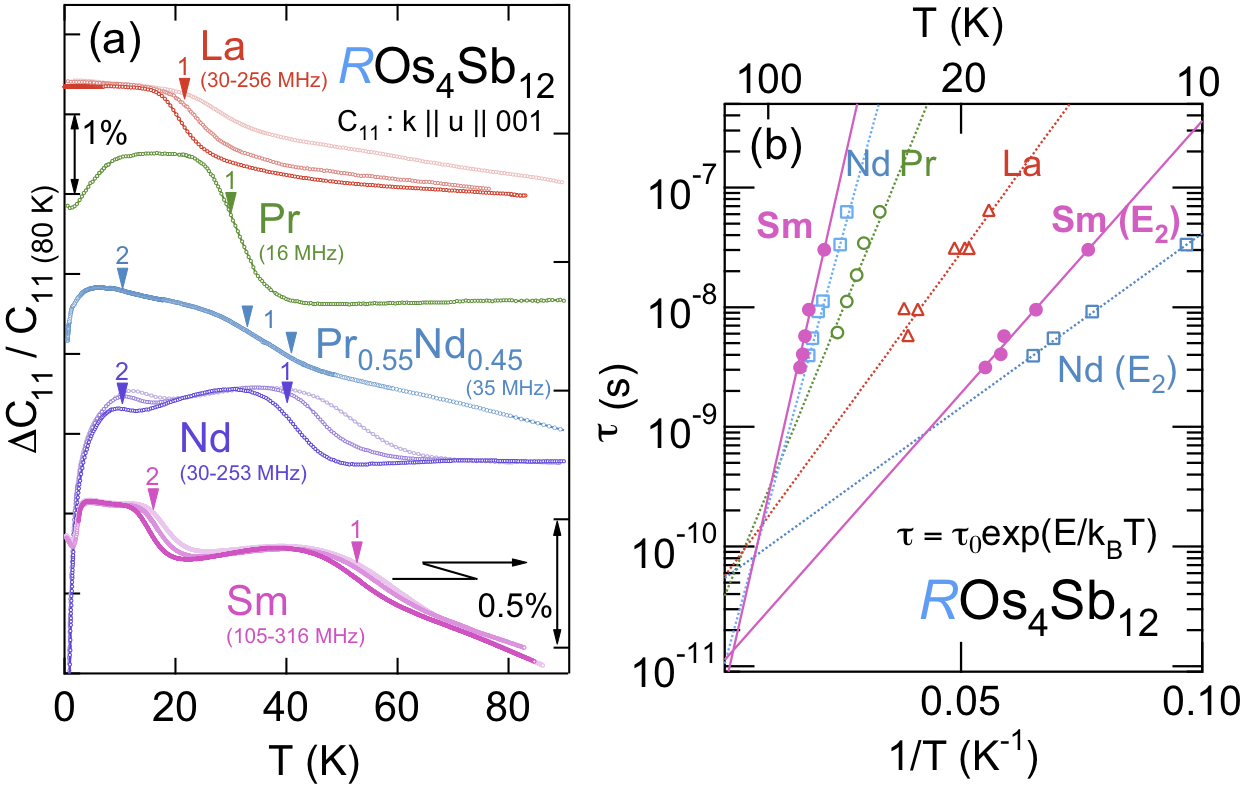
図39 (a) $Ln$Os$_4$Sb$_{12}$の弾性定数$C_{11}$に現れる超音波分散の系統変化と(b) アレニウスプロット

表6 充填スクッテルダイトに於ける格子定数，デバイ温度，アインシュタイン温度，電子比熱係数と超音波分散から得られたパラメータの比較[71]}

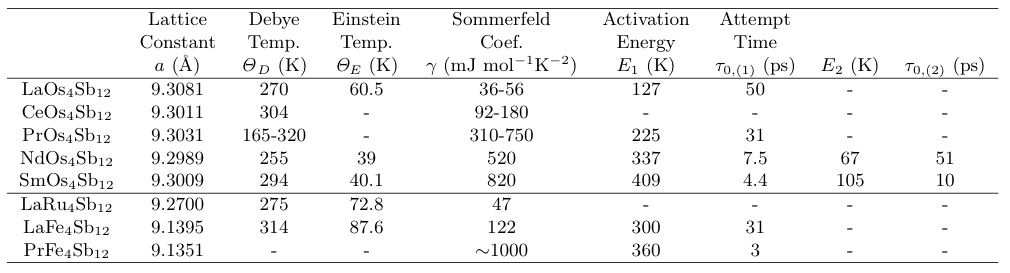
まず活性エネルギー$E$の系統変化をみてみると，$R$Os$_4$Sb$_{12}$において希土類をLaからSmに変えると$E_{1}$が上昇し，$¥tau_{0, (1)}$が減少する傾向がある．電子比熱係数$¥gamma$は上昇している．一般に電子有効質量を増大させる機構が近藤効果などの多体効果であるとすれば，その特性温度$T^¥ast$（近藤温度に対応する）は$¥gamma$の増大とは逆相関である．一方，近藤効果で抑えられていた磁気相関が，$T_{¥rm K}$が下がることで回復し，磁気揺らぎによってエントロピーが食われて$¥gamma$が下がる場合は正の相関となる．よって後者の観点から，本研究において見いだされた$¥gamma$と正の相関を持つ活性エネルギーは電子有効質量増強の特性温度と間接的に結びついている可能性はあると言える．

次にアインシュタイン温度と活性エネルギーを比較してみよう．ここで，SmとNdは二つの超音波分散に対応する二つの活性エネルギーを持つが[75]，それぞれ低い方の活性エネルギーを抽出する．そうすると，$Ln$Os$_4$Sb$_{12}$系のアインシュタイン温度と活性エネルギー（低エネルギー側）がちょうどファクター2の関係にあるようにみえる．この関係は服部らによって提唱された伝導電子と局所フォノンとの間の新しいエネルギー散逸機構を示唆する[76]．もし電子-フォノン結合[77]による電子比熱係数の増大とラットリングエネルギースケールの変化が間接的に関わっているとすれば，磁場に鈍感な電子比熱係数の起源としてラットリングに伴う局所電荷揺らぎと伝導電子との結合が現実味を帯びてくる．

今後の課題として，先ずはSmOs$_4$Sb$_{12}$の結晶場基底状態の問題に決着をつける必要がある．そのためには$T_{¥rm K} ¥sim 10$ Kよりも高温領域における弾性定数の磁場依存性などを解析する必要がある．また，実験的困難はあるものの，Smの同位体をエンリッチした結晶を作成し，非弾性中性子回折実験によって結晶場を直接観測することが望ましい．また，超音波分散を生む局所電荷自由度と価数揺動が結合している可能性もある．これに関しては同位体効果や，Smに対する他の希土類元素の置換効果，圧力効果等の研究[78]が有力な情報を与えてくれるかもしれない．

(おわりに・謝辞・参考文献に続く）