第4章　緩和の現象論

ここまで駆け足で，$f$電子化合物の弾性応答の典型例について紹介してきたが，これまでの議論に於いては，超音波による歪みは電子系に対する「静的な」摂動として取り扱った．超音波の周波数$¥omega$はたかだか数百MHz程度であるから，一般に電子系の緩和時間$¥tau$よりも充分長い（$¥omega ¥tau ¥ll 1$）．この場合，パルスエコー法の実験で得られる「音速」とは，図21に示すフォノンの分散関係における音響フォノンモードの$k = 0$の傾き，即ちフォノンの「群速度」

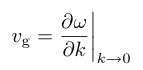(28)

に該当する．
一方，相転移近傍における臨界現象や価数揺動，ラットリングに伴う局所電荷ゆらぎ等に起因し，電子系の緩和時間が超音波の周波数に近づく場合（$¥omega ¥tau ¥sim 1$）は, 電子-フォノン相互作用を通して音速（と超音波吸収）にも緩和現象が現れる．ここで位相速度を

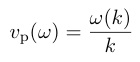(29)

と定義すると，音速に分散がある場合，群速度と位相速度が一致しなくなることを意味する．これを「分散領域」と呼ぼう．以下の議論では分散領域($v_{¥rm g} ¥neq v_{¥rm p}$)において周波数$¥omega$に依存する位相速度$v_{¥rm p}$を考える．また，$C = ¥rho v^2$の関係式で結ばれる弾性定数（弾性率）も周波数に依存する動的弾性定数（弾性率）$C(¥omega)$として定義できる ．それは複素弾性率の実数成分として現象論的に理解できる．以下にはその一般式を示す．

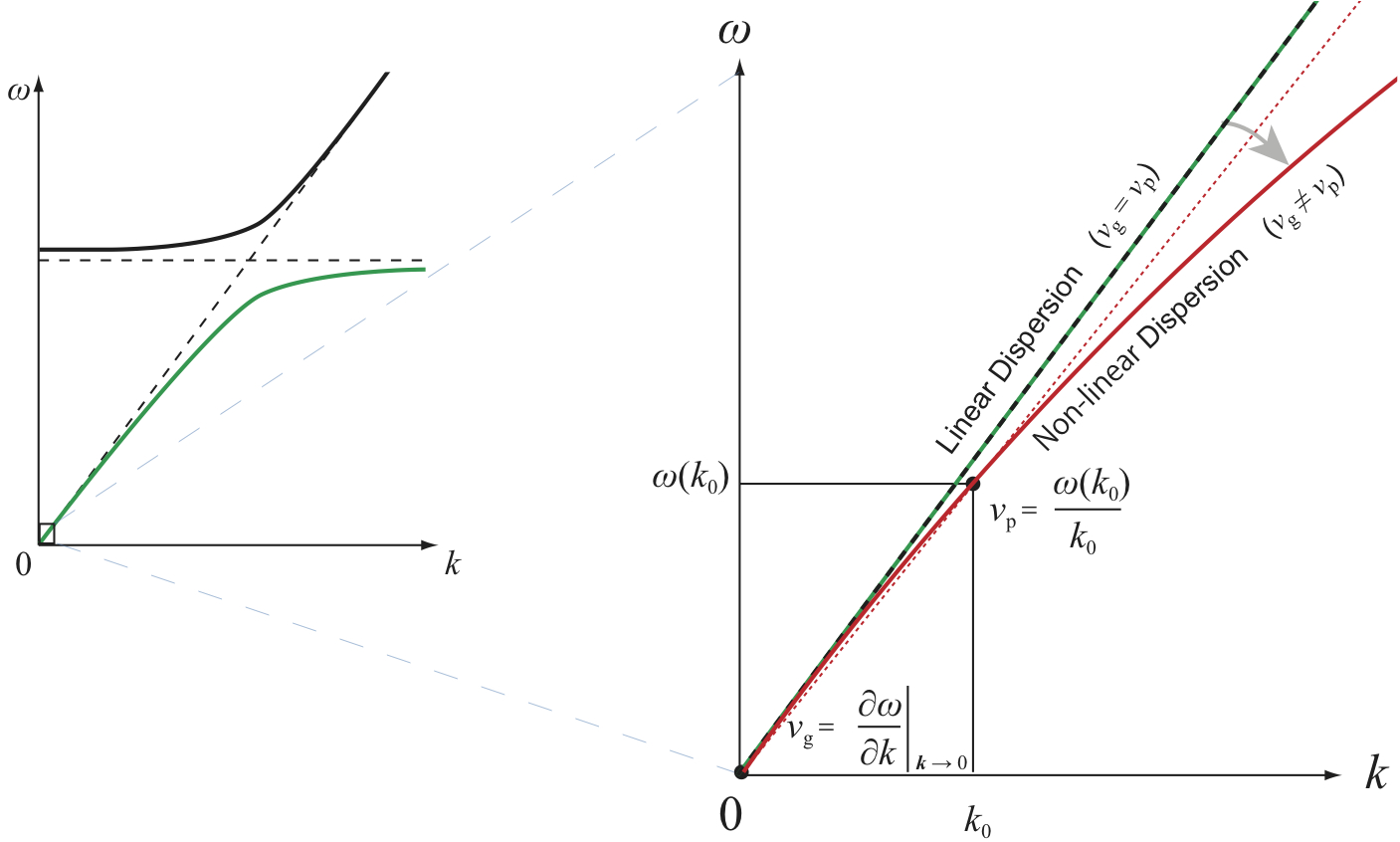
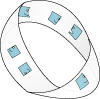
図21 左はカゴ状物質における低エネルギー領域のフォノン分散関係の模式図．右は群速度$v_{¥rm g}$と位相速度$v_{¥rm p}$の概略図（ここでは$k ¥sim 0$近傍の曲率の変化を誇張して描いている）．

4.1 複素弾性率

熱平衡状態に外部から磁場$H$, 電場$E$, 歪み$¥epsilon$, 温度$T$などをかけて平衡状態からずらすとき，再び熱平衡状態に近づいていく過程を緩和現象という．平衡状態と瞬間力が「静的」な内部状態であるのに対して，緩和現象ではさらに系の「動的」な性質を記述する必要がある. 例えば熱力学では状態方程式等を与えて系の性質を規定しなければならないように，動的な現象論では緩和（応答）函数をまず与えてから系の状態を規定していかなくてはならない．

たとえばある秩序変数$¥eta$を仮定し，それが歪みや応力といったマクロな物理量の影響を受ける場合を考える~¥cite{45}．非平衡状態で$¥eta$は時間と共に変化し，平衡値$¥eta_0$に近づいてゆく．この緩和過程を表す最も簡単な場合は

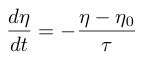(30)

と記述できる．$¥tau$は典型的な緩和時間である．平衡値$¥eta_0$も同様に歪みの影響を受ける．上式は$t = 0$で$¥eta = ¥eta'$であったとすると，

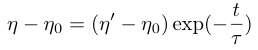(31)

のように指数函数的に系の緩和が起こる事を表している．緩和函数（または応答函数）が時間と共に指数函数的に減衰する例は自然界にしばしば観られ，特に誘電体の誘電緩和現象で起きるデバイ型緩和現象は，磁化の緩和を観る交流磁化率や局所電荷ゆらぎの緩和を観る超音波分散の解析に類推して用いられる．

さて，系に音波が伝搬することにより歪みが弾性波の角周波数$¥omega$で周期的に断熱変化すると仮定する．

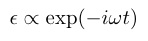(32)

すると，秩序変数の平衡値$¥eta_0$も弾性波の影響を受けるが，$¥eta$もまたある位相差を伴って変化するはずである．
その結果，式(30)は

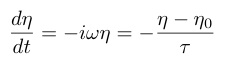(33)

と書け，

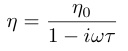(34)

となる．
弾性率は一般的な感受率(応答/外場)として理解すると(応力/歪み)$= ¥partial¥sigma / ¥partial¥epsilon$で与えられる~¥cite{46}．

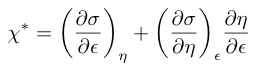(35)

ここで第１項は静的弾性率，第２項は動的弾性率である．
式(33)を代入すると

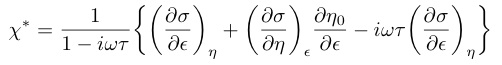(36)

ここで，
$(¥partial¥sigma/¥partial¥epsilon)_{¥eta}+(¥partial¥sigma/¥partial¥eta)_{¥epsilon}(¥partial¥eta/¥partial¥epsilon)$
は充分に遅い緩和に対する応力の歪み微分であるから，歪みの変化が充分に遅い緩和過程($¥omega ¥tau ¥ll 1$)で平衡状態が壊れないとすると$¥eta$は常に平衡値$¥eta_0$をとるため，単純に$(¥partial¥sigma/¥partial¥epsilon)_{eq.}$と書ける．ここで

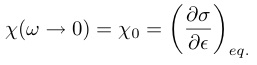(37)

を低周波極限（即ち静的弾性率）と定義する．
一方，歪みの変化が非常に速い場合($¥omega ¥tau ¥gg 1$)では$¥eta$は系の変化に追いつけずに一定$¥eta_{¥infty}$に保たれる．その中間の周波数つまり$¥omega ¥tau ¥sim 1$の近傍では$¥eta$の変化は歪みのそれよりも位相が遅れ，応力の変化として観測される．ここで

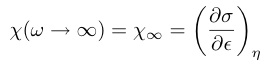(38)

を高周波極限と定義する．
式(37) と(38)を用いると，(36)は

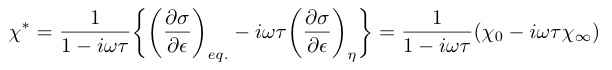(39)

と書ける．

先述の通り，$¥chi$は弾性率に限らず，一般的に交流磁化率や誘電緩和などの緩和現象を解析する感受率と類推できる．現実を描写するため，弾性率を実部と虚部に分ける．複素弾性率$¥chi^{¥ast}$と複素音速度$v^{¥ast}$の関係式

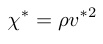(40)

と，複素音速度と吸収係数αの関係式

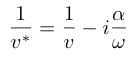(41)

より，実際の超音波測定では複素弾性率$¥chi^{¥ast}=¥chi_{¥rm Re.}+i ¥chi_{¥rm Im.}$の実部は動的弾性定数$C(¥omega)$，虚部は超音波吸収係数$¥alpha(¥omega)$として観測される．

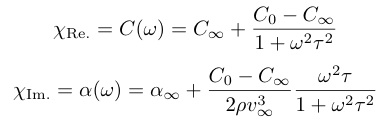(42,43)

図22は充填スクッテルダイトLaOs$_4$Sb$_{12}$の超音波分散の研究で得られた活性エネルギーと緩和時間を用いて計算された動的弾性率（左軸）と超音波吸収係数（右軸）である．図22の下に示すのはアレニウス型の緩和時間の温度依存性である．超音波の測定周波数$¥omega$（左軸から延ばした直線）と系（ラットリング）の緩和時間$¥tau$がマッチングする領域（共鳴条件$¥omega ¥tau ¥sim 1$）で，実部の弾性率は低周波極限$C_0$から高周波極限$C_{¥infty}$へ増大し，虚部の超音波吸収は極大を示す．これが次章で示すラットリングに伴う超音波分散の現象論的な解釈である．

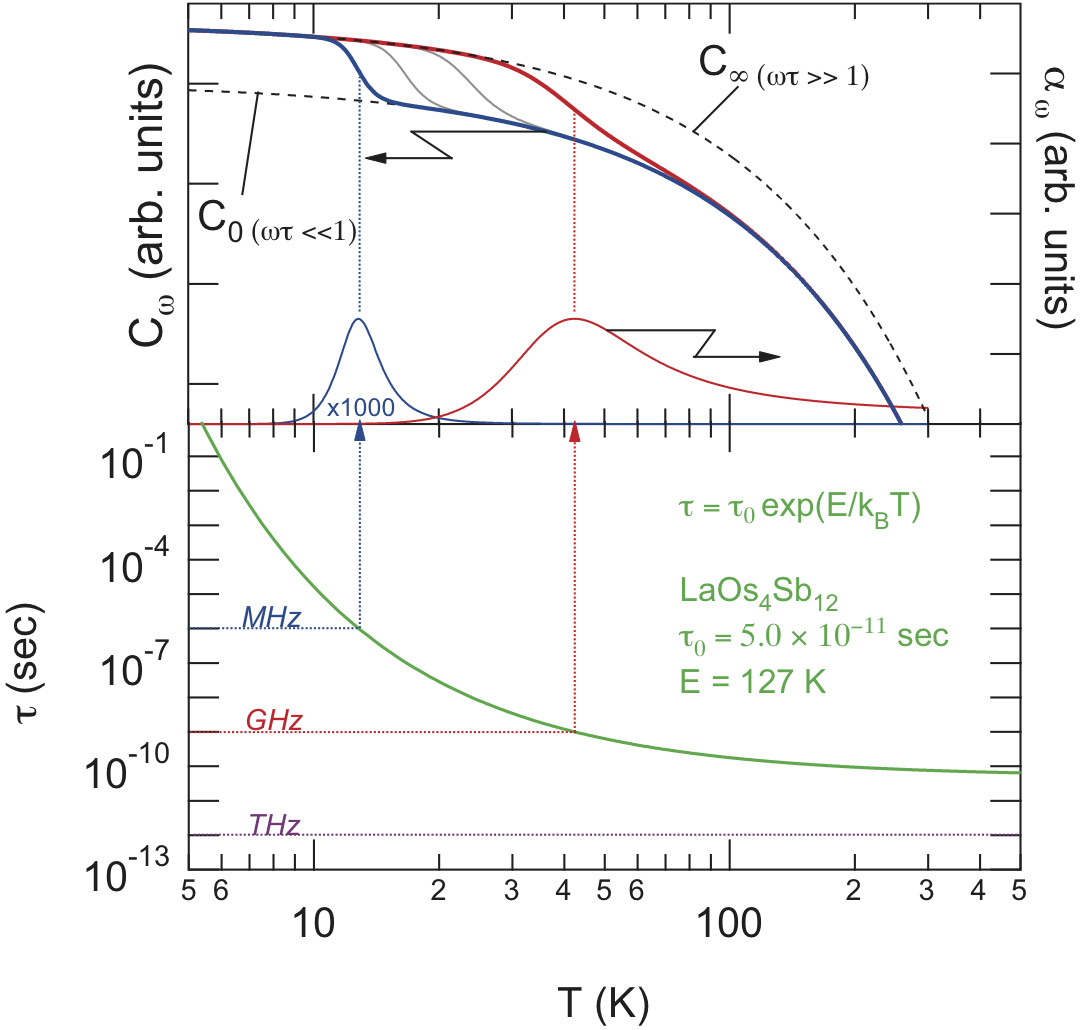
図22 LaOs$_4$Sb$_{12}$の超音波分散の現象論的な解釈.

4.2 音響フォノンと音速の関係（位相速度と群速度についての蛇足）

先述した通り，パルスエコー法で得られる音速とは，非分散領域（音速に分散が無い領域）においては，超音波パルスの波束の間隔 [s]と伝搬経路長[m]から求められる速度を意味し，これはフォノンの群速度$v_{¥rm g}$に該当する．一般に音速という場合はこれを指すことが多い．一方，位相比較法で得られる「音速」とは，一定の位相をもった波面が伝搬する速度のことを指し，これはフォノンの位相速度$v_{¥rm p}$に該当する．先述の通り，実際の測定では一定位相を持つ連続波をパルス化して入射しており，入射波束が持つ位相と基準信号の位相差を検出し，位相差を一定（即ち波数$k$を一定）に保つように周波数$¥omega$に負帰還をかけ，位相速度の相対変化$¥Delta v_{¥rm p}(¥omega)/v_{¥rm p}(¥omega)$を周波数の相対変化$¥Delta ¥omega/¥omega$として読み替えている．分散領域では群速度と位相速度が一致しない($v_{¥rm g} ¥neq v_{¥rm p}$)が，非分散領域では一致する($v_{¥rm g} = v_{¥rm p}$)ため，位相比較法は両者を測定していることになる．

ここで慧眼なる読者は気づかれたかもしれないが，結晶にモノクロマティックな（単一周波数を持った）超音波を入射する場合，分散領域ではある周波数$¥omega$に対応するフォノンの位相速度が変化し，超音波が伝搬しなくなることが懸念される．例えば図22にあるように，緩和時間がアレニウス型の温度依存性を示す時，厳密にモノクロマティックな超音波を用いた実験を行った場合，群速度と位相速度が異なるので，パルスエコー間隔を追った実験では緩和に伴い位相速度が変化し，パルス波の大部分が吸収されるため，音速の低周波極限から高周波極限への変化は不連続なデータとして観測されるはずである．しかし，実際は超音波トランスデューサの特性上，ある帯域幅を持った波群が入射されているため，我々が実験で作り出せる超音波は完全なモノクロ波ではない．よって，分散領域でも音速の相対変化をある程度連続的に追う事ができる．位相比較法では分散領域において位相速度が変化しても，周波数分布の裾の周波数帯の波が伝搬し続けるので，位相信号を見失う事無く追跡し，負帰還によって変調される周波数の相対変化から位相速度の相対変化を観測することができる．

(第5章1節に続く）