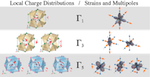
Topics: 超音波からみた多極子・ラットリング
3. 歪みと弾性定数,四極子感受率
3-1 歪みと弾性エネルギー
第3章 歪みと弾性定数,四極子感受率
物理的に意味があるのは音速ではなく,単位体積当たりに蓄えられる弾性エネルギーを表す「弾性定数」である.実験からは音速とC = ρ v2の関係で弾性定数(SI系では[J m-3],CGS単位系では[erg cm-3]の次元)が得られる.物質の密度ρが一定であると仮定した時,弾性定数の絶対値は音速の絶対値によって決まり,ヤーン・テラーエネルギーや四極子相互作用の結合定数を見積もる際に重要になる.一方,弾性定数の単位を圧力の単位[Pa]や[dyn/cm2]で表す場合もある.こちらは圧力効果を論じる場合や圧縮率(バルクモジュラス)との比較を行う際に有効かもしれない .
本章ではまず局在性が強い(混成効果が弱い)f 電子系について四極子感受率の定式化を行う.結論を先に言ってしまうと,それは量子力学の二次摂動を用いた,電気双極子と誘電率,あるいは磁気双極子と帯磁率の関係式と全く同じである.超音波が作る歪み場と結合するのは電気四極子であるから,波動函数に適用する演算子のランクが双極子から1つだけ上がり,物理量がベクトルからテンソルに変わる以外は何ら特別なことは無い.だから一度でも感受率の計算をやったことのある方は読み飛ばしてもらって構わない.
3.1 歪みと弾性エネルギー
物質は外場に対して何らかの応答を示す.例えば,磁場H に対して磁束密度B,電場E に対して電束密度D,応力Tに対して歪みS が発現する.それらの関係を表1に示す.
Table 1 物理テンソル・特性テンソル・外場のトライアドと,応答する多極子
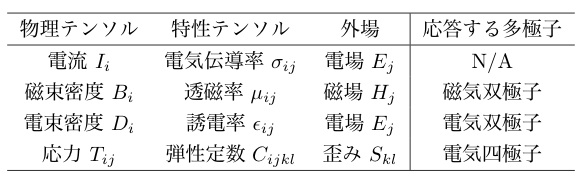
一般に固体物理学で結晶が物理テンソル I の場の下にある場合,それによる観測量eと結晶の性質に由来する(結晶の異方性によって簡略化された)特性テンソルdの間には以下の関係がある.
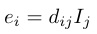 (1)
(1)
ここで,添え字i, j (=1,2,3)は座標成分を表し,添え字の数は階数(ランク)と呼ぶ.
1階ランクのテンソル(即ちベクトル)同士を結びつける物理量dijは2階ランクのテンソルであり,マトリクス型式で表される.
さて,超音波による音速測定から得られる物理量は表1の弾性(スティフネス)定数である.これは物質の応力に対する歪みにくさ,即ち「かたさ」に対応する量で,歪みSも応力Tも2階ランクの極性テンソルであるから,これらを繋ぐ特性テンソルの弾性定数は4階ランクの極性テンソルである.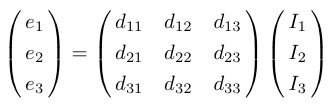 (2)
(2)
応力Tijはi面に働くj方向の力をあらわす.本稿では今後,誘電率は登場しないので,普段私たちが論文で用いている表記に変更し,歪みをεkl,応力をσijと再定義すると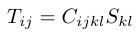 (3)
(3)
テンソル量Cijklは対称で,その要素は添字の順番に依らないから,以下のようなVoigtの表記で書き換えることができる.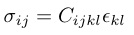 (4)
(4)
11 → 1, 22 → 2, 33 → 3, 23,(32) → 4, 31(13) → 5, 12(21) → 6.
マトリクス形式で式(4)を表してみよう.
ここで,空白部分は対称要素Cij=Cjiであるため省略した.さらに,物体に働く応力は釣り合っており,回転モーメントは無いとすると,応力も歪みも対称となり,もともと34 = 81個あった4階テンソルの要素の数が21個に簡約化される.さらに結晶がある対称操作に対して不変であるとすると,特性テンソルは簡約化される.独立な弾性定数の要素は結晶の対称性に応じて減り,最も対称性の高い立方対称では独立な弾性定数はC11, C12, C44のたった3個になる.ここでは群論の詳細については割愛するが,三斜晶から立方晶までの結晶対称性において対称操作によって残る独立な弾性定数と,その基底函数をまとめたものを表2に示す.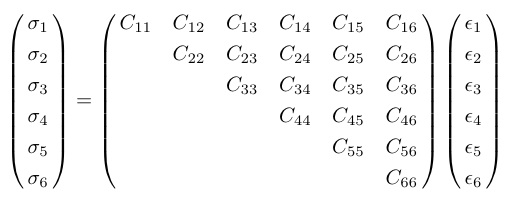 (5)
(5)
Table 2. 様々な結晶系における独立な弾性定数 [6]

Table 3. 立方晶系における超音波の伝搬・変位方向と弾性定数の関係

下では簡単のため,結晶構造が立方晶の場合について考える.一般に,歪みは次のような対称テンソルで定義される.
ここでuiは変位ベクトルであり,歪みは無次元量であることがわかる.上式で定義された歪みは,x, y, zの二次多項式と同じ変換をする(i,j=1,2,3 → x,y,zと置き直すと解り易い)から,点群Oの既約表現と同じ変換をする対称歪みεΓを求めることができる.表3に立方晶系における超音波の伝搬・変位方向と,誘起される歪み,観測される弾性定数の関係を示した.立方晶系の弾性エネルギーはフックの法則により,弾性定数と対称化された歪みを用いて以下のように書ける.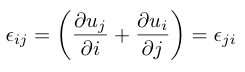 (6)
(6)
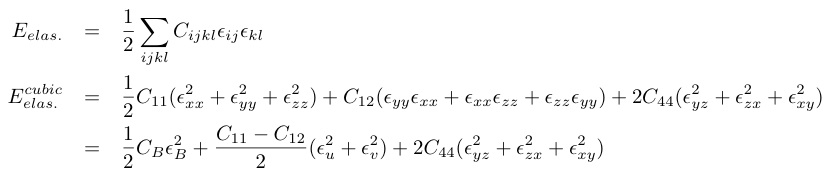 (7)
(7)
ここでCB = (C11+2C12)/3はバルクモジュラス で結晶対称性を保持するΓ1 対称性の体積歪みεB = εxx+εyy+εzzに対応し図4に示すような単極子・電気十六極子と結合する.(C11-C12)/2, C44はそれぞれΓ3, Γ5対称性の対称歪みに対する四極子の応答に対応する.磁場中の横波超音波には歪みに加えて,格子の回転が弾性エネルギーに寄与する.そのため超音波の伝搬方向と磁場方向の関係に依っては,弾性エネルギーに差が生じる.本稿では割愛する.
(第3章3.2節に続く)