第３章　 歪みと弾性定数，四極子感受率

3.2 四極子感受率

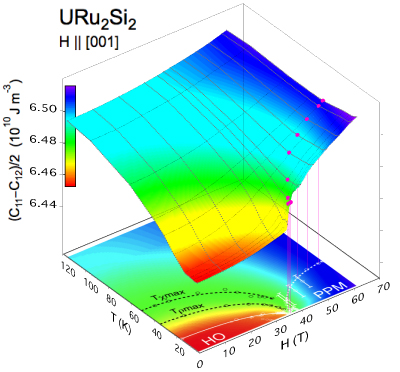
弾性定数の結晶場効果による温度変化は一般的に四極子感受率として理解できる．四極子感受率は歪み場を摂動として系に加えた場合の四極子モーメントの応答である．これは外部磁場に対する磁気モーメントの応答としての帯磁率と単純に類推できる．以下でその一般式を導く．

結晶中に入射された超音波は結晶格子をわずかに歪ませる．電子状態が四極子を持っている場合，四極子-歪み相互作用を媒介に歪みは結晶場ポテンシャルV_CEFに変調を与えて電子系と結合する．そのエネルギー変化は極めて小さな摂動として取り扱うことができる．

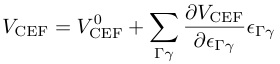(8)

V_CEF⁰は無摂動状態の結晶場ポテンシャル，Γ_γは点群の既約表現の基底を表し，ε_Γγは対称歪みである．四極子-歪み相互作用のハミルトニアンH_QSはV_CEFを歪みの1次まで展開し，第２項の展開係数をウィグナー・エッカートの定理より等価演算子で置き換えると次のように書ける，

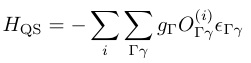(9)

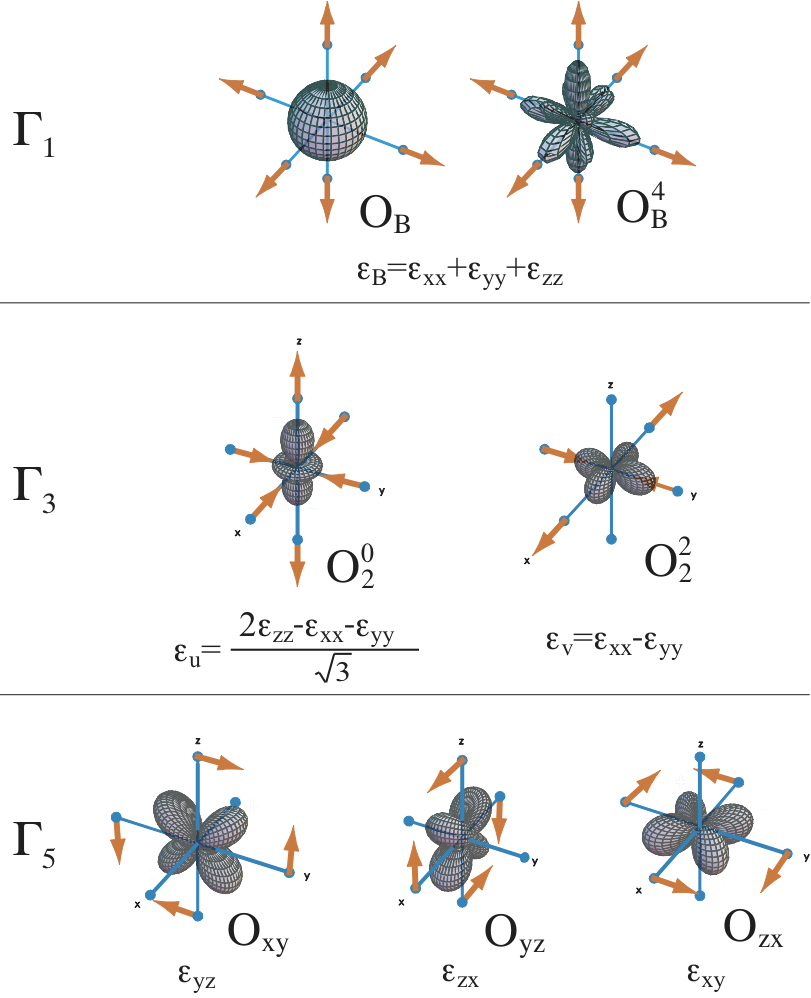
g_Γは四極子-歪み相互作用の結合定数，O_Γγは局在f電子の電気四極子の電荷分布を表す等価演算子で四極子演算子と呼ばれる．電気四極子の大きさは量子軌道の異方的な空間的広がり面積と電荷の積に比例する．希土類イオンのf軌道は角運動量で量子化されているので，四極子の大きさは演算子

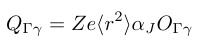(10)

を用いて計算できる．ここにZeは希土類イオンの有効電荷，<r²>は希土類イオンでのf軌道の動径方向の自乗平均，α_Jはスティーブンス因子である．以下，四極子演算子O_Γを単純に「四極子」と呼ぶことにする．

Fig. 4 対称歪みと結合する多極子

さて，点群の各既約表現に対応する四極子は角運動量J_x, J_y, J_zの線形結合で書き表され，等価演算子法を用いて以下のように記述できる．

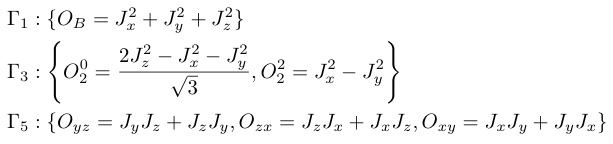(11)

さらに，四極子同士にも伝導電子やフォノンを媒介としてRKKY的な相互作用が働いているものとし，これを四極子間相互作用のハミルトニアンをH_QQとして次のように表すことができる．

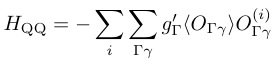(12)

ここでg_Γ'は四極子のサイト間相互作用定数であり，< O_Γγ>は或るサイトi に注目したとき他の全てのサイトの四極子を期待値で置き換える分子場近似を表す．

4f 電子系で立方晶の場合，摂動を受けた結晶場に対する摂動ハミルトニアンは次の様に書ける．

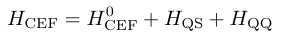(13)

後の説明のため、結晶場ハミルトニアンは、Lea-Leask-Wolfの良く知られた表式[7]を用いておく。

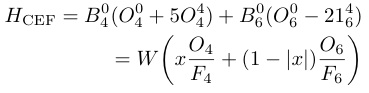(14)

ここで，Wはスケール因子，x (|x|≦1)は４次と６次の項の係数比で，F₄とF₆は全角運動量Jによって決まる．O_n^mはスティーブンスの等価演算子で，これは結晶場ポテンシャルを球面調和函数で多重極展開すると得られる．全角運動量Jの結合式としての以下のようなテンソル演算子で記述できる．

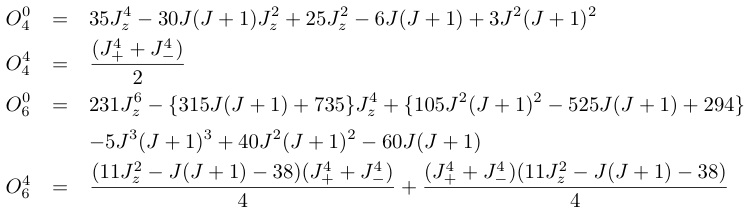(15)

一方，四極子間相互作用が無視できない場合はε_Γγの代わりに有効歪み$ε_Γγ^effを考えると都合が良い．

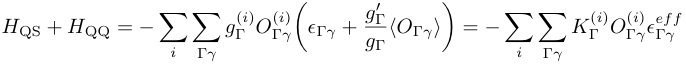(16)

K_Γは相互作用を繰り込んだ場合の結合定数である,１イオンに対する電子系の摂動のエネルギーは歪みの二次まで計算し，

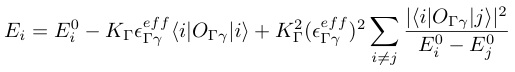(17)

と表すことができる．E_i⁰は四極子-歪み相互作用が存在しない場合の結晶場状態 $|i ¥rangle$のエネルギーである．
次に，弾性定数の表式を得るために自由エネルギーについて考える．系の全自由エネルギーは,

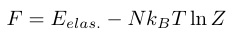(18)

と表される．右辺一項目は結晶の弾性エネルギー，二項目はf 電子系全体のエネルギーである．Nは単位体積あたりのf 電子の総数を表し，Zは状態和である．弾性定数は自由エネルギーを歪みε_Γγで二階微分し，ε_Γγ→0の極限をとることで求められる．

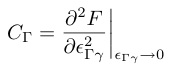(19)

C_Γ⁰は四極子-歪み相互作用が働かないときの弾性定数を表しており，主に格子（音響フォノンの非調和性）からの寄与によるバックグラウンドとなる． χ_Γは四極子感受率（歪み感受率）とよばれ，

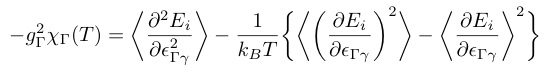(20)

で与えられる．ブラケットはボルツマンの熱平均を意味する．第一項はヴァンブレック項であり，四極子O_Γγの行列要素の非対角要素からの寄与を表す．この項は低温で温度に依らず一定となる．第二項はキュリー項であり，O_Γγの対角要素からの寄与を表す．四極子演算子にあまり馴染みが無い方も，上記の表式には見覚えがあるだろう．これは量子力学の二次摂動を用いた磁化$M$と，磁気感受率としての帯磁率χ_Mの関係と全く同じである．四極子モーメントの熱平均は次のように書ける.

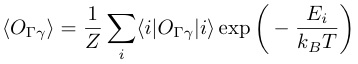(21)

いま，系が常磁性相における平衡状態で，四極子モーメント間に相互作用は働いておらず，摂動ハミルトニアンとしてH_QSだけが効くと考えた場合，四極子感受率は,

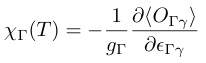(22)

となる．従って，四極子感受率とは単位歪み当たりに誘起される電気四極子を意味し，これは一様な磁場中で磁気双極子モーメントの平均値として定義される磁化の関係に対応していることがわかる．
基底状態が四極子に対して縮退している場合（即ち，基底状態の波動函数を四極子演算子に適用したとき，その行列要素が対角成分を持つ場合）低温で温度の逆数(1/T)に比例する「弾性定数の減少（軟化）」が現れる．以後，結晶場によるf 電子の四極子自由度に起因する弾性定数の軟化を表す用語として「ソフト化」と定義しよう．

(第３章3.3節に続く）