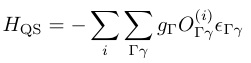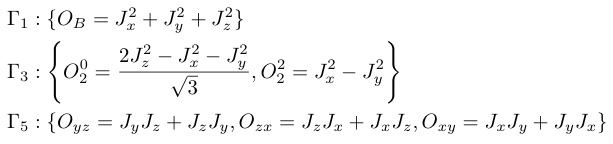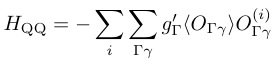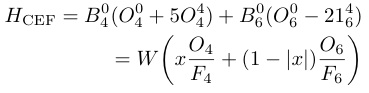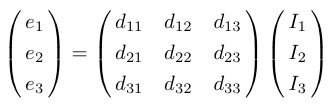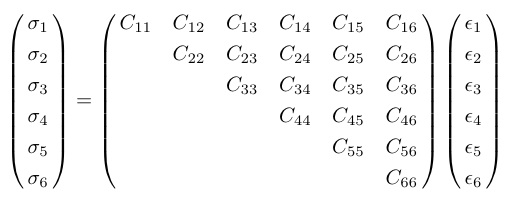本稿は、新学術領域研究（研究領域提案型）「重い電子系の形成と秩序化」が主催した「重い電子系若手秋の学校’１１」のテキストブックをHTML化したものです。物性研究における超音波実験の役割を簡単にレビューします。

---

第１章　はじめに

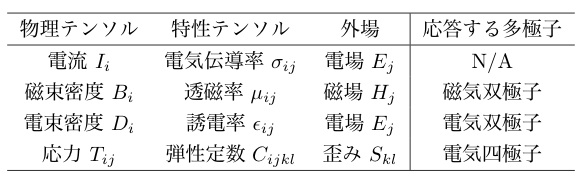
わたしたちは物性を調べるとき，物質に様々な外場をかけ，それに対する物質の持つ様々な自由度の応答を観測する．例えば磁性を調べる場合，最も簡単な方法は物質に磁場を加え，物質中のスピン自由度の応答をその周りに巻いたコイル等で観測する方法である．それでは，わたしたちが扱う強相関電子系に於いて「超音波測定」とはどのような外場を加え，何の応答を観測できるのだろうか？その質問に大雑把に答えるとしたら

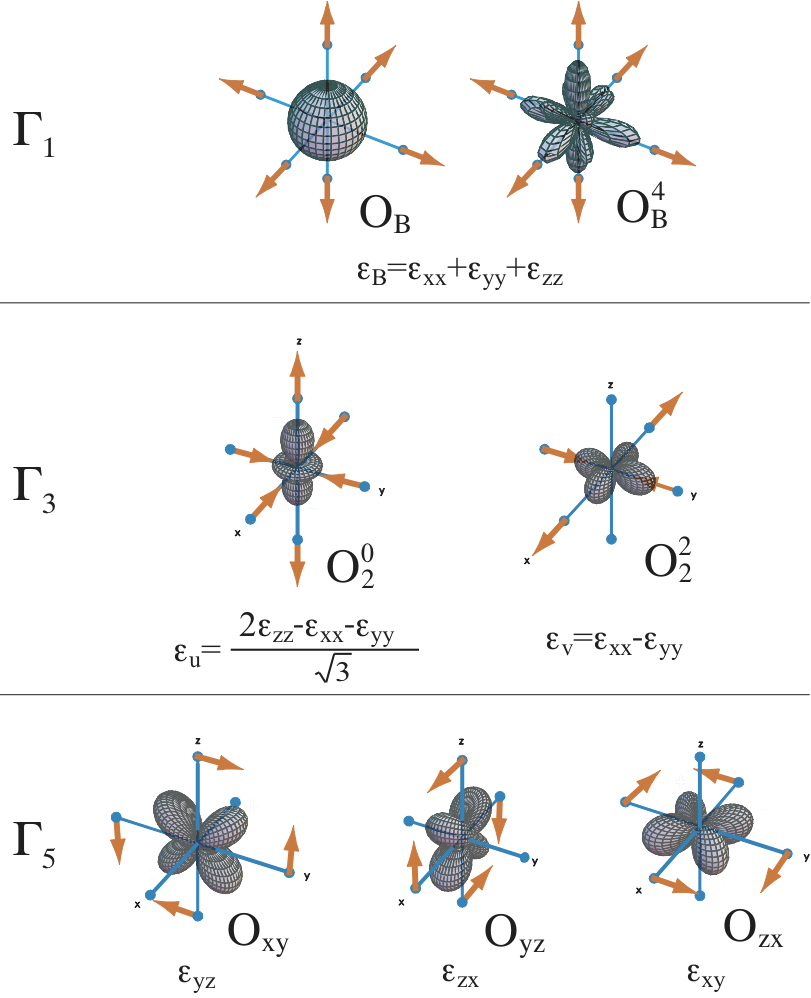
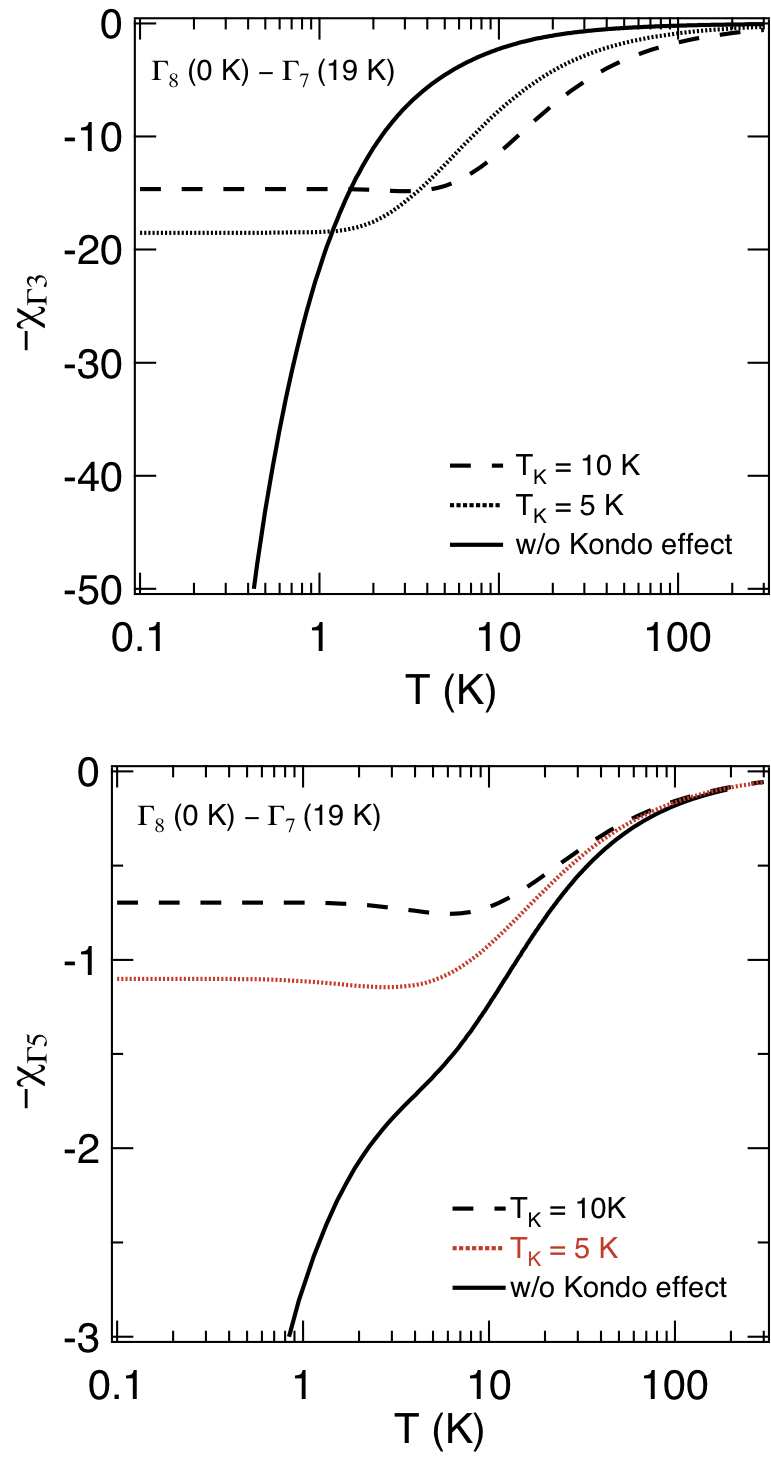
「超音波測定は物質中に歪み場を加え，電気四極子の応答を観測する手法である．」

と言えるだろう．

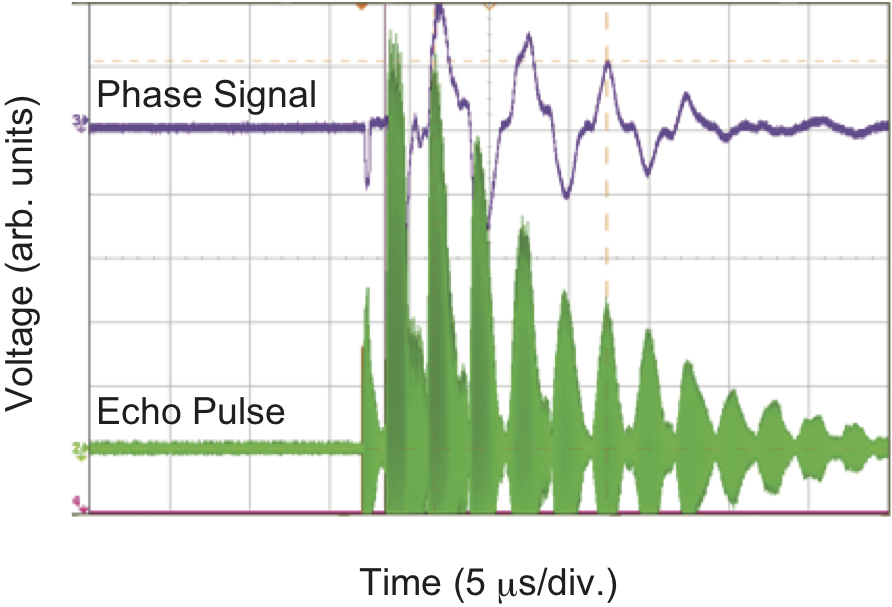
超音波は弾性波として固体中を伝搬する．局所的にその弾性波をみると，結晶中に然るべき対称性を持った歪み場が作り出されている．電子系はその歪み場を，ポテンシャルの変化として感じる．もし固体が完全結晶（※１） で周期的な格子を持つ場合，そのポテンシャルは結晶対称性によって周期函数で表される．超音波には縦波と横波が存在するため，様々な対称性の歪み場を加えることができる．超音波計測とは，いわば系のポテンシャルを外から直接揺さぶり，電子系（ならびに格子系）の応答を四極子感受率（あるいは歪み感受率）として観測する手法であり，磁気モーメントの応答に対応する帯磁率，エントロピーに対応する比熱とともに物性物理学における有効な測定手段の一つである．

そのため，超音波を用いて得られる「弾性定数」という基本的物理量は固体物理学の教科書には必ずと言っていいほど登場する．しかしながら，「磁性」や「誘電性」を観測する実験手法に比べ，超音波実験とそこから得られる物理には，正直なところ馴染みが少ないという学生諸君が多いのではなかろうか．確かにキッテル先生のIntroduction to Solid State Physicsでは一時期，弾性定数の章が割愛されていたし(※２），物性物理学の門を叩いた学生は自分の測定した比熱や磁化を手っ取り早く計算したいので，固体物理の教科書の「弾性」の章は読み飛ばしている可能性が高い．

そこで，本稿では学生の皆さんに「超音波で固体の電子状態を観る」ことにもっと馴染んでもらうべく，超音波で得られる物理量の持つ意味と，それを重い電子系や多極子秩序，ラットリング等を示す系に適用したときに得られるデータの解釈の仕方について，実験屋の視点から基礎的な解説をし，最後に最近著者が行っている充填スクッテルダイト化合物のラットリングの研究について，超音波実験から得られた知見を紹介する．

本稿が学会や論文で超音波の実験結果をみる際の手助けになれば幸いである.

(第二章に続く）

注釈
※１　 人類が手にすることができる最も「完全」に近い結晶はシリコンの単結晶である．しかし最近，極低温弾性定数測定によって１モル当り10¹⁴個程度の単原子空孔の存在が明らかになった. [1]
※２　7th Edition以降で復活

本稿は、新学術領域研究（研究領域提案型）「重い電子系の形成と秩序化」が主催した「重い電子系若手秋の学校’１１」のテキストブックをHTML化したものです。

第２章　超音波実験の測定手法

2.1 パルス法

先ず，超音波実験の測定手法と測定の勘所を至極簡単に述べよう．超音波測定では，固体中を伝搬する弾性波の音速と吸収を測定する．パルス法と呼ばれる方法は固体の音速を測定する最もポピュラーな方法である．良く研磨された測定試料面に各種の接着剤によりトランスデューサを接着し，トランスデューサの共振周波数に合った連続波発信器を用意する．そこから出力された電気信号をゲートに通して充分に短い幅（200-500 [ns]）に切り，ドライブ・パルスとしてトランスデューサに入力する．トランスデューサによってパルス信号は超音波パルスに変換され，試料中を弾性波（歪み波）として伝搬する．試料の両端面で反射を繰り返した超音波パルスはトランスデューサにより再度電気信号に変換され，検出器へ送られる．オシロスコープでその信号の時間変化を監視すると，図1のような「超音波パルスエコー」が得られる．「エコー」とは山びこ現象で次々に聞こえる「こだま」そのものである．理想的なパルスエコーならばその振幅は exp(-βt)に比例して減衰する．t [s]は入射信号からの遅延時間である.

超音波が伝搬する経路長を，試料端で反射したエコーが届く時間間隔で割れば，超音波の音速$v$の絶対値が得られる．βは単位長さ当たりの超音波吸収係数α [dB m^-1]、音速v [m s^-1]との間にβ = α/vの関係を持つ．ここで，ドライブ・パルスはほぼ矩形のエンベロープを持っているが，電気音響変換の過程で歪みを生じたり、トランスデューサを試料に貼付ける為の接着剤による影響でエンベロープのエッジが丸みを帯びてくる。特に電気機械結合定数の高いLiNbO₃を圧電素子として用いた場合，エコー信号の立ち上がりを正確に知ることが難しくなるため，正確な絶対値の測定には直接試料表面に圧電結晶をスパッタリングする方法や圧電高分子トランスデューサをスピンコート法で塗布するなどの工夫が必要である.いずれにしても音速の絶対値の測定精度には限界があり，うまく測定しても数%の誤差が生じてしまう．

Fig. 01 超音波エコーの観測例：URu₂Si₂の横波弾性定数C₄₄モードの超音波エコーのスナップ写真．
（厚さ100 μmのLiNbO₃ウエーハをトランスデューサに用い，３倍高調波の105 MHzで観測した．）

Fig. 02 位相比較法で扱う信号のタイムチャート（概念図）

Fig. 03 超音波位相比較法のブロックダイアグラム

 

2.2 位相比較法

量子系の状態を反映したより微小な音速の変化を検出するためには，エコー信号を検出するのではなく，位相信号を用いることで高い分解能を達成することができる．これは位相比較法と呼ばれる手法である．位相比較法については様々なところで解説があるので[2,3] ，その詳細については省くが，ここでの勘所は音速の変化を基準信号からの遅延（位相差）として観測し（図２)，位相差をゼロ検出し，先程の発信器に負帰還をかけることで，音速の相対変化を信号発生器の周波数の相対変化に読み替えるところにある．即ち，原理的には測定周波数が高ければ高いほど，分解能が向上することになる．また，ゼロ検出法を用いることで，測定系における非線形性の影響を受けにくく，Δ v/v 〜 10^-7のきわめて高い分解能の測定が可能となる．この高い分解能は，特にSi単結晶内に存在する単原子空孔の量子状態の測定[4]や，音響ドハース効果などの極微小な量子振動の検出に有効である．我々が用いている測定系のブロックダイアグラムを図3に示す．これとは別に周波数を固定して生の位相差信号をデジタルストレージに保存し，そこから音速の相対変化と吸収係数を同時に算出する方法もある[5]．この方法は若干分解能で劣るものの，積分器による負帰還を行わないため，音速の変化が著しい場合やパルス磁場下など短い時定数で測定を行う必要がある場合に有効である．

(第３章に続く）

本稿は、新学術領域研究（研究領域提案型）「重い電子系の形成と秩序化」が主催した「重い電子系若手秋の学校’１１」のテキストブックをHTML化したものです。

第３章　 歪みと弾性定数，四極子感受率

 

3.2 四極子感受率

弾性定数の結晶場効果による温度変化は一般的に四極子感受率として理解できる．四極子感受率は歪み場を摂動として系に加えた場合の四極子モーメントの応答である．これは外部磁場に対する磁気モーメントの応答としての帯磁率と単純に類推できる．以下でその一般式を導く．

結晶中に入射された超音波は結晶格子をわずかに歪ませる．電子状態が四極子を持っている場合，四極子-歪み相互作用を媒介に歪みは結晶場ポテンシャルV_CEFに変調を与えて電子系と結合する．そのエネルギー変化は極めて小さな摂動として取り扱うことができる．

(8)

V_CEF⁰は無摂動状態の結晶場ポテンシャル，Γ_γは点群の既約表現の基底を表し，ε_Γγは対称歪みである．四極子-歪み相互作用のハミルトニアンH_QSはV_CEFを歪みの1次まで展開し，第２項の展開係数をウィグナー・エッカートの定理より等価演算子で置き換えると次のように書ける，

(9)

g_Γは四極子-歪み相互作用の結合定数，O_Γγは局在f電子の電気四極子の電荷分布を表す等価演算子で四極子演算子と呼ばれる．電気四極子の大きさは量子軌道の異方的な空間的広がり面積と電荷の積に比例する．希土類イオンのf軌道は角運動量で量子化されているので，四極子の大きさは演算子

(10)

を用いて計算できる．ここにZeは希土類イオンの有効電荷，<r²>は希土類イオンでのf軌道の動径方向の自乗平均，α_Jはスティーブンス因子である．以下，四極子演算子O_Γを単純に「四極子」と呼ぶことにする．

Fig. 4 対称歪みと結合する多極子

さて，点群の各既約表現に対応する四極子は角運動量J_x, J_y, J_zの線形結合で書き表され，等価演算子法を用いて以下のように記述できる．

(11)

さらに，四極子同士にも伝導電子やフォノンを媒介としてRKKY的な相互作用が働いているものとし，これを四極子間相互作用のハミルトニアンをH_QQとして次のように表すことができる．

(12)

ここでg_Γ'は四極子のサイト間相互作用定数であり，< O_Γγ>は或るサイトi に注目したとき他の全てのサイトの四極子を期待値で置き換える分子場近似を表す．

4f 電子系で立方晶の場合，摂動を受けた結晶場に対する摂動ハミルトニアンは次の様に書ける．

(13)

後の説明のため、結晶場ハミルトニアンは、Lea-Leask-Wolfの良く知られた表式[7]を用いておく。

(14)

ここで，Wはスケール因子，x (|x|≦1)は４次と６次の項の係数比で，F₄とF₆は全角運動量Jによって決まる．O_n^mはスティーブンスの等価演算子で，これは結晶場ポテンシャルを球面調和函数で多重極展開すると得られる．全角運動量Jの結合式としての以下のようなテンソル演算子で記述できる．

(15)

一方，四極子間相互作用が無視できない場合はε_Γγの代わりに有効歪み$ε_Γγ^effを考えると都合が良い．

(16)

K_Γは相互作用を繰り込んだ場合の結合定数である,１イオンに対する電子系の摂動のエネルギーは歪みの二次まで計算し，

(17)

と表すことができる．E_i⁰は四極子-歪み相互作用が存在しない場合の結晶場状態 $|i ¥rangle$のエネルギーである．
次に，弾性定数の表式を得るために自由エネルギーについて考える．系の全自由エネルギーは,

(18)

と表される．右辺一項目は結晶の弾性エネルギー，二項目はf 電子系全体のエネルギーである．Nは単位体積あたりのf 電子の総数を表し，Zは状態和である．弾性定数は自由エネルギーを歪みε_Γγで二階微分し，ε_Γγ→0の極限をとることで求められる．

(19)

C_Γ⁰は四極子-歪み相互作用が働かないときの弾性定数を表しており，主に格子（音響フォノンの非調和性）からの寄与によるバックグラウンドとなる． χ_Γは四極子感受率（歪み感受率）とよばれ，

(20)

で与えられる．ブラケットはボルツマンの熱平均を意味する．第一項はヴァンブレック項であり，四極子O_Γγの行列要素の非対角要素からの寄与を表す．この項は低温で温度に依らず一定となる．第二項はキュリー項であり，O_Γγの対角要素からの寄与を表す．四極子演算子にあまり馴染みが無い方も，上記の表式には見覚えがあるだろう．これは量子力学の二次摂動を用いた磁化$M$と，磁気感受率としての帯磁率χ_Mの関係と全く同じである．四極子モーメントの熱平均は次のように書ける.

(21)

いま，系が常磁性相における平衡状態で，四極子モーメント間に相互作用は働いておらず，摂動ハミルトニアンとしてH_QSだけが効くと考えた場合，四極子感受率は,

(22)

となる．従って，四極子感受率とは単位歪み当たりに誘起される電気四極子を意味し，これは一様な磁場中で磁気双極子モーメントの平均値として定義される磁化の関係に対応していることがわかる．
基底状態が四極子に対して縮退している場合（即ち，基底状態の波動函数を四極子演算子に適用したとき，その行列要素が対角成分を持つ場合）低温で温度の逆数(1/T)に比例する「弾性定数の減少（軟化）」が現れる．以後，結晶場によるf 電子の四極子自由度に起因する弾性定数の軟化を表す用語として「ソフト化」と定義しよう．

(第３章3.3節に続く）

本稿は、新学術領域研究（研究領域提案型）「重い電子系の形成と秩序化」が主催した「重い電子系若手秋の学校’１１」のテキストブックをHTML化したものです。

第３章　超音波実験の測定手法

 

3.4 近藤効果を取り入れた四極子感受率（横波超音波）の一例（CXcal-excel）

結晶場と近藤効果の共存系における各種物理量の計算プログラム``CXcal-excel''が，酒井治先生によって配布されている[23]．このプログラムは磁性不純物の結晶場を考慮したアンダーソン・ハミルトニアンから出発し，Non Crossing Approximation（NCA）と呼ばれる自己無撞着摂動論を用いて立方対称結晶場にあるCe³⁺ (J = 5/2)の１イオン感受率の温度依存の数値データとグラフを簡便に与えてくれる.

図11に結晶場レベルがΓ₈(0 K)-Γ₇(19 K)で，近藤温度T_Kを5 Kと10 Kに設定したときの四極子感受率-χ_Γ3と-χ_Γ5の温度依存性を示す．横軸は温度の対数で表している．実線は前節で計算したNCA計算を用いない１イオン感受率である．図12には結晶場レベルがΓ₇(0 K)-Γ₈(38 K)のときの同様の結果を示す．この後の解説のために申し添えると，結晶場分裂幅をこれらの値にした理由は，最終章で紹介するSmOs₄Sb₁₂の四極子応答を解釈するためである．Γ₇基底モデルの結晶場分裂幅はΓ₈基底モデルの丁度2倍の値に設定しているので，Γ₈基底モデルの温度軸を2倍にスケールすれば同じ分裂幅の感受率を比較できる．結晶場分裂幅Δに対してT_Kが半分くらいになるとΓ₈基底モデルではキュリー項によるソフト化が急激に抑えられ，逆にΓ₇基底モデルでは高温領域でソフト化が増大する．例えばΓ₅対称性の四極子感受率-χ_Γ5はT_K = 5-10 K程度を仮定した場合. Γ₇とΓ₈基底状態のいずれかを定性的には区別できなくなっていることがわかる．（図11,12下図の破線を比較してみよう．）.

図11 Γ₈(0 K)-Γ₇(19 K)の結晶場状態を持つCe³⁺ J = 5/2の4f 電子系に対する近藤効果を考慮した場合と考慮しない場合の四極子感受率の比較

図12 Γ₇(0 K)-Γ₈(38 K)の結晶場状態を持つCe³⁺ J = 5/2の4f 電子系に対する近藤効果を考慮した場合と考慮しない場合の四極子感受率の比較

(第３章3.5節に続く）

本稿は、新学術領域研究（研究領域提案型）「重い電子系の形成と秩序化」が主催した「重い電子系若手秋の学校’１１」のテキストブックをHTML化したものです。

第３章　 歪みと弾性定数，四極子感受率

物理的に意味があるのは音速ではなく，単位体積当たりに蓄えられる弾性エネルギーを表す「弾性定数」である．実験からは音速とC = ρ v²の関係で弾性定数（SI系では[J m^-3]，CGS単位系では[erg cm^-3]の次元）が得られる．物質の密度ρが一定であると仮定した時，弾性定数の絶対値は音速の絶対値によって決まり，ヤーン・テラーエネルギーや四極子相互作用の結合定数を見積もる際に重要になる．一方，弾性定数の単位を圧力の単位[Pa]や[dyn/cm²]で表す場合もある．こちらは圧力効果を論じる場合や圧縮率（バルクモジュラス）との比較を行う際に有効かもしれない ．

本章ではまず局在性が強い（混成効果が弱い）f 電子系について四極子感受率の定式化を行う．結論を先に言ってしまうと，それは量子力学の二次摂動を用いた，電気双極子と誘電率，あるいは磁気双極子と帯磁率の関係式と全く同じである．超音波が作る歪み場と結合するのは電気四極子であるから，波動函数に適用する演算子のランクが双極子から1つだけ上がり，物理量がベクトルからテンソルに変わる以外は何ら特別なことは無い．だから一度でも感受率の計算をやったことのある方は読み飛ばしてもらって構わない．

3.1 歪みと弾性エネルギー

物質は外場に対して何らかの応答を示す．例えば，磁場H に対して磁束密度B，電場E に対して電束密度D，応力Tに対して歪みS が発現する．それらの関係を表１に示す．

Table 1 物理テンソル・特性テンソル・外場のトライアドと，応答する多極子

一般に固体物理学で結晶が物理テンソル I の場の下にある場合，それによる観測量eと結晶の性質に由来する（結晶の異方性によって簡略化された）特性テンソルdの間には以下の関係がある．

(1)

ここで，添え字i, j (=1,2,3)は座標成分を表し，添え字の数は階数(ランク)と呼ぶ．
１階ランクのテンソル（即ちベクトル）同士を結びつける物理量d_ijは２階ランクのテンソルであり，マトリクス型式で表される．

(2)

さて，超音波による音速測定から得られる物理量は表1の弾性（スティフネス）定数である．これは物質の応力に対する歪みにくさ，即ち「かたさ」に対応する量で，歪みSも応力Tも2階ランクの極性テンソルであるから，これらを繋ぐ特性テンソルの弾性定数は4階ランクの極性テンソルである．

(3)

応力T_ijはi面に働くj方向の力をあらわす．本稿では今後，誘電率は登場しないので，普段私たちが論文で用いている表記に変更し，歪みをε_kl，応力をσ_ijと再定義すると

(4)

テンソル量C_ijklは対称で，その要素は添字の順番に依らないから，以下のようなVoigtの表記で書き換えることができる.

11 → 1, 　22 → 2,　33 → 3,　23,(32) → 4,　31(13) → 5,　12(21) → 6.

マトリクス形式で式(4)を表してみよう．

(5)

ここで，空白部分は対称要素C_ij=C_jiであるため省略した．さらに，物体に働く応力は釣り合っており，回転モーメントは無いとすると，応力も歪みも対称となり，もともと3⁴ = 81個あった4階テンソルの要素の数が21個に簡約化される．さらに結晶がある対称操作に対して不変であるとすると，特性テンソルは簡約化される．独立な弾性定数の要素は結晶の対称性に応じて減り，最も対称性の高い立方対称では独立な弾性定数はC₁₁, C_12, C₄₄のたった３個になる．ここでは群論の詳細については割愛するが，三斜晶から立方晶までの結晶対称性において対称操作によって残る独立な弾性定数と，その基底函数をまとめたものを表2に示す.

Table 2. 様々な結晶系における独立な弾性定数 [6]

Table 3. 立方晶系における超音波の伝搬・変位方向と弾性定数の関係

下では簡単のため，結晶構造が立方晶の場合について考える．一般に，歪みは次のような対称テンソルで定義される．

(6)

ここでu_iは変位ベクトルであり，歪みは無次元量であることがわかる．上式で定義された歪みは，x, y, zの二次多項式と同じ変換をする(i,j=1,2,3 → x,y,zと置き直すと解り易い)から，点群Oの既約表現と同じ変換をする対称歪みε_Γを求めることができる．表3に立方晶系における超音波の伝搬・変位方向と，誘起される歪み，観測される弾性定数の関係を示した．立方晶系の弾性エネルギーはフックの法則により，弾性定数と対称化された歪みを用いて以下のように書ける．

(7)

ここでC_B = (C₁₁+2C₁₂)/3はバルクモジュラス で結晶対称性を保持するΓ₁ 対称性の体積歪みε_B = ε_xx+ε_yy+ε_zzに対応し図4に示すような単極子・電気十六極子と結合する．(C₁₁-C₁₂)/2, C₄₄はそれぞれΓ₃, Γ₅対称性の対称歪みに対する四極子の応答に対応する．磁場中の横波超音波には歪みに加えて，格子の回転が弾性エネルギーに寄与する．そのため超音波の伝搬方向と磁場方向の関係に依っては，弾性エネルギーに差が生じる．本稿では割愛する．

(第３章3.2節に続く）