
我々は実験系の研究グループです。
物性物理学は多様な物質現象の中から新たな物理の基本法則を見つけ出すことを目指す学問です。
通常は熱散乱のベールに隠されている量子力学的な基底状態を、
極低温環境下における物性測定で詳らかにするべく、日々研究を続けています。
ここでは現在進行中の研究テーマと、実験手法・技術についてご紹介します。
研究内容
拡張多極子による動的応答
UNi4Bのトロイダル秩序状態における新しい電流誘起磁化現象
5f 電子系の磁性と超伝導
URu2Si2における隠れた秩序と微弱反強磁性
c-f混成によって誘発されるURu2Si2の格子不安定性(パルス強磁場下超音波測定)
重い電子系超伝導体UBe13の超伝導混合状態における磁気特性
112希薄系における局所的非フェルミ液体異常
4f 電子系の磁性と超伝導
単サイト四極子近藤効果の検証:
Y1-xPrxIr2Zn20 の弾性応答に観る 対数的温度変化
重い電子系超伝導体UPt3における極低温磁化測定
EuIn2P2における磁場中比熱測定
SmOs4Sb12 の静水圧力下超音波測定
磁場に鈍感な重い電子系スクッテルダイト化合物 SmOs4Sb12 のラットリング
(ラットリングを示す充填スクッテルダイト化合物の磁性と超伝導)
TmM2Si2(M: 遷移金属)系の磁性
非フェルミ液体的振る舞いを示す YbRh2Si2 の極低温磁性
研究手法/実験装置(一覧)
極低温基礎物性測定
キャパシタンス式極低温精密磁力計を用いた磁化測定(100μW希釈冷凍機)
SQUID磁束計による磁化測定、交流磁化率測定
緩和法比熱測定(HELIOX)
電気抵抗測定(Handmade希釈冷凍機)
高圧下物性測定
インデンターセルによる高圧下電気抵抗・AC磁化測定
MPMS用インデンター&ピストンシリンダセルによる静水圧下DC磁化測定
ピストンシリンダセル断熱法比熱測定
超音波物性測定
位相比較法(ヘテロダイン検波)を用いた弾性定数測定
蒸着装置&ネットワークアナライザ(超音波圧電素子制作)
微視的測定
中性子散乱実験
共鳴X線散乱実験
ミュオンスピン回転・緩和・共鳴(muSR)実験
物質合成
テトラアーク炉によるチョクラルスキー法単結晶試料育成
プラズマジェット炉による多結晶試料育成
フラックス法による単結晶試料育成
放電加工機
物質評価(X線構造解析・EPMA等)
中性子散乱実験
中性子は電荷を持たずにスピンを持つ粒子です。微小磁石としての性質があり、これを物質に打ち込むと、物質中の電子磁気モーメントや原子核と力を及ぼし合って散乱されます。中性子散乱実験では、中性子の波としての性質である回折現象を利用し、物質中の磁気モーメントの配列や運動を調べることができます。私達のグループでは、年に 3~4 回、東大物性研究所の共同利用として日本原子力研究所で実験を行っています。
研究用原子炉JRR-3M |
汎用三軸型中性子分光器 |
実験風景 |
実験終了後の反省会 |
[Method] キャパシタンス式磁力計を用いた極低温精密磁化測定
低温で磁化を測定する方法としては、試料をピックアップコイルの中で動かして誘導起電力を測る誘導法と試料に交流磁場をかけて応答をみる交流法が、これまで主に用いられてきました。しかし、これらの方法では摩擦や誘導電流による発熱があるため、1 K以下の極低温下で精密な測定を行うことは非常に困難でした。私たちのグループでは、榊原教授(現、東大物性研教授)、卒業生の田山孝氏(現、東大物性研助手)らが中心となって独自の磁力計を開発し、希釈冷凍機温度領域(40 mK ~ 5 K)で9万エルステッド(参考までに、地磁気の大きさは0.1エルステッド以下)までの磁場掃引による高感度磁化測定を可能にしました。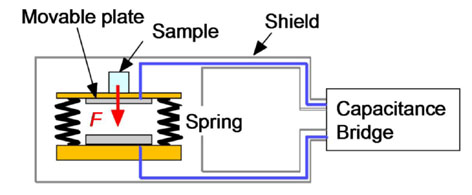
キャパシタンス式磁力計の動作原理図
この磁力計は、磁性体に働く力が磁化と磁場勾配に比例することを利用したものです。磁性体に働く力に比例して平行平板コンデンサー(電極間距離約 0.1 mm)の可動電極が動き、静電容量が変化するので、この静電容量を高精度キャパシタンスブリッジで正確に測ることによって磁化がわかるという仕組みです。つまり、下図のようなキャパシタンス式の「バネばかり」で磁性体に働く力を測定しているのです。試料をほとんど動かす必要が無いので発熱が無いことが、極低温領域での静的磁化測定を可能にした理由です。この装置の開発により、たとえば、重い電子系の異方的超伝導状態における熱平衡磁化の振る舞いを初めて明らかにすることができました。私達は現在、静水圧下および1軸応力下で磁化測定を可能にするため、さらに装置の機能を拡張しています。
キャパシタンスセル |
圧力セル搭載型改良キャパシタンスセル |
極低温磁化測定システムを組み込んだ |
断熱セル内部 |
テトラアーク炉
プラズマ炉、3極および4極アーク炉、アニール炉などを用い、金属間化合物の合成と単結晶化を行います。テトラアーク炉
プラズマジェット炉
放電加工機
物質評価(X線構造解析・EPMA等)
4極(テトラ)アーク炉外観 |
ベルジャー部 |
単結晶が成長する様子 |
引き上げられた単結晶の例 |
高温大気炉 |
シリコニット炉 |
物質合成
プラズマ炉、3極および4極アーク炉、アニール炉などを用い、金属間化合物の合成と単結晶化を行います。テトラアーク炉
プラズマジェット炉
放電加工機
物質評価(X線構造解析・EPMA等)
4極(テトラ)アーク炉外観 |
ベルジャー部 |
単結晶が成長する様子 |
引き上げられた単結晶の例 |
高温大気炉 |
シリコニット炉 |
[TOPICS] 重い電子系超伝導体UBe13の超伝導混合状態における磁気特性
1911年にカマリン・オンネスによって発見された超伝導現象に関する理解は、1957年のBCS(Bardeen-Cooer-Schrieffer)理論の提唱により、ほとんど解決したかに思われました。しかし、1980年代になると、セリウムやウランを含む重い電子系化合物による超伝導や、有機超伝導、高温超伝導の発見(1986年)をきっかけに、BCS理論では説明できない、いわゆる『非BCS超伝導体』が次々と発見されるようになりました。これらの非BCS超伝導体は、上記のような重い電子系化合物 をはじめとする強い電子相関を持つ系、すなわち『強相関電子系』において多く見られ、『異方的超伝導ギャップ』や『多重超伝導相』、BCS理論では説明不可能な『異常な上部臨界磁場Hc2』、さらには『磁性と超伝導の共存』など、数多くの興味深い現象を示します。特に、『磁性と超伝導の共存』は、本来水と油のような関係であると考えられてきた『磁性』と『超伝導』という物理現象を結びつけるという意味で、これまでの常識を覆すものです。
これらの非BCS超伝導を研究する上での、根本的課題の一つは『強い斥力がはたらくはずのこれらの強相関電子系においてなぜ超伝導が起こるのか?』ということです。超伝導現象は、ある電子と別の電子が引かれ合って対を成し(Cooper対)、そのような電子対を物質中の巨視的な数の電子が一斉に形成するというような一種のボーズ凝縮のようなものとして解釈できます。これは微視的には、ボーズ粒子としての何らかの『量子ゆらぎ』がフェルミ粒子である電子同士間にはたらき、相互作用することで電子対を形成するという解釈がなされます。BCS理論で説明可能な従来型の超伝導体の多くは格子振動、つまり「フォノン」を媒介としたものであると考えられています。電子は当然のことながら電荷を持ちますから、電子同士にはクーロン斥力がはたらきます。つまり超伝導になるにはクーロン斥力に打ち勝つだけの『引力』が必要ということになります。私たちの研究室で取り組んでいるセリウムCeやウランUを含む重い電子系物質では、4f, 5f電子が主な物性を担っており、それらの物質中の電子は通常の金属において伝導を担うs, p電子に比べ、相当に大きなクーロン斥力を感じていると考えられます。これらの電子相関の強い系おいて通常のBCS超伝導が実現するのは難しいと考えられています。なぜなら、フォノンを媒介としたBCS超伝導が起こるためには、電子同士がかなり近づく必要があるからです。(厳密には片方の電子からもう片方の電子を相対的にみたときの電子の存在確率はデルタ関数的であり、距離が同じところの存在確率が最も大きくなります)それにも関わらず、なぜ重い電子系化合物には超伝導を示すものがあるのでしょうか?言い換えれば、『重い電子系超伝導体をもたらす量子揺らぎ』は何なのでしょうか?
重い電子系化合物に超伝導をもたらす起源の可能性のひとつとして量子臨界点の存在が挙げられます。重い電子系化合物には、低温において反強磁性秩序や強磁性秩序、さらには多極子秩序といった多彩な秩序状態を示すものが多くあります。そして、それらの秩序-無秩序転移温度は圧力や元素置換などによって絶対零度近傍に制御することが可能です。こうして得られた秩序-無秩序転移温度が絶対零度に落ち込む点は『量子臨界点』とよばれます。この量子臨界点近傍では、熱揺らぎは押さえられ、電子系における量子揺らぎのはたらきが顕著になります。そして、最近の研究から、それらの量子揺らぎが超伝導の引力に起因しているのではないかと考えられるようになりました。たとえば、反強磁性を示す物質であれば、反強磁性揺らぎが超伝導を導く要因になっているのではないか、と考えるわけです。実際に、重い電子系反強磁性体における量子臨界点近傍において非BCS超伝導が発見されている例が最近では多く見つかっています。
このようなエキゾチックな超伝導の起源をさらに深く探るにはどうしたらよいのでしょうか?反強磁性体における超伝導を例にとって考えてみましょう。それらの物質においてはその量子臨界点近傍で反強磁性ゆらぎが強いわけですから、Cooper対を形成しようする電子同士においても反強磁性的な相互作用、つまりスピンを反平行向きにしようとする相互作用がはたらきます。したがって、反平行スピンをもつCooper対が形成されやすいということになります。このような反平行スピンからなるCooper対をもつ超伝導は、スピン一重項(spin-singlet pairing)超伝導とよばれます。同様に、平行スピンをもつCooper対からなる超伝導はスピン三重項(spin-triplet pairing)とよばれます。電子対波動関数を考えるとき、全体の波動関数は単純にはスピン部分と軌道部分の積から成り立ちます。電子はフェルミ粒子ですので、Cooper対の電子対波動関数は粒子の入れ替えに対し反対称であることが要請されます。電子対のスピンが平行であるとするとスピン部分の波動関数は粒子の入れ替えに対して対称であるため、軌道部分の波動関数は反対称(奇パリティ:p波やf波)となります。一方で、反平行スピンについては、軌道部分の波動関数は粒子の入れ替えに対して対称なもの(偶パリティ :s波やd波)になります。また、物質中では原子は結晶を成しているため、その結晶場中における引力相互作用も物質の対称性を反映したものになるはずであり、軌道部分の波動関数はその引力相互作用の対称性を反映します。つまり異方的な引力相互作用が異方的超伝導ギャップとして超伝導ギャップの対称性に反映されます。したがって、Cooper対のパリティがsingletであるかtripletであるかということや、電子対の軌道部分の波動関数がどのようなものであるか、ということは超伝導の起源を探るために非常に重要な情報だということが言えます。
私たちの研究室では特に、5f電子をもつウラン系の重い電子系超伝導体における超伝導メカニズムに興味を持ち、その超伝導対称性を明らかにすることを目的としていろいろな物性測定からアプローチしています。
本研究室が取り組んでいるUBe13もウラン系非BCS重い電子系超伝導体の一つです。UBe13は立方晶の結晶構造をもち、低温で通常の金属よりも遥かに大きな電子比熱係数を示す重い電子系化合物ですが、1983年にスイスのOttらによって このUBe13が超伝導状態を示すことが発見されました[1]。超伝導転移温度以下の比熱の温度依存性がT3的で3Heにおけるスピン三重項p波超流動状態で実現しているとされているABM (Anderson-Brinkman-Morel) 状態のものに類似していることから、UBe13においてもスピン三重項が実現しているのではないかと提唱され、ウラン系化合物における最初の異方的超伝導として一躍脚光を浴びました [2]。また、NMR(Nuclear-Magnetic-Resonance)スピン格子緩和率 [3]、磁場侵入長 [4]、さらには超音波吸収 [5] の温度依存性からも、超伝導ギャップが点(ポイントノード)または線(ラインノード)でゼロになるような異方的超伝導ギャップを示唆するということが報告されました。しかし、結局のところ、これらの結果を総合して見てみても、超伝導ギャップがどのような対称性を持っているのかについて、今のところ決着はついていません。また、超伝導のパリティを決定する上で重要な微視的なスピン帯磁率の結果においても、現在のところNMR Knightシフトの結果とmuon-SR Knight shiftの結果は一致していません。つまり、超伝導対がスピン一 重項なのか、それともスピン三重項なのかさえはっきりしていないというのが現状です。このように、発見から既に四半世紀以上も経過した現在もなお、UBe13の超伝導はその超伝導対称性が明らかになっていないだけではなく、その他の多くの未解決な問題を抱えています。本研究室では、UBe13における超伝導対称性とその風変わりな超伝導の性質を解明するため、最近原子力機構先端研の芳賀芳範教授が作成に成功した純良な試料を用い、超伝導状態における極低温DC磁化測定をはじめ、磁場中比熱測定など多方面からのアプローチを行っています。
参考文献
[1] H. R. Ott et al., Phys. Rev. Lett. vol. 50 (1983) 1595.
[2] H. R. Ott et al., Phys. Rev. Lett. vol. 52 (1984) 1915.
[3] D. E. MacLaughlin et al., Phys. Rev. Lett. vol. 53 (1984) 1833.
[4] D. Einzel et al., Phys. Rev. Lett. vol. 56 (1986) 2513.
[5] B. Golding et al., Phys. Rev. Lett. vol. 55 (1985) 2479.















