D3清水君が優秀講演賞を受賞しました

我が研究室のD3清水悠晴君が、大阪大学で行われた重い電子系国際ワークショップTOKIMEKI 2011において、"Unusual Magnetic Properties in Superconducting State of UBe13"の発表を行い、Student Oral Presentation Awardを受賞しました。おめでとう!パチパチパチパチ☆
ACCESS
所在地 (郵便物宛先)
| 〒060-0810 札幌市北区北10条西8丁目 北海道大学大学院理学研究科 物理学専攻 強相関電子磁性1 極低温グループ |
研究室
| 名 称 | 部 屋 番 号 | Tel. |
| 学生居室1(日髙居室) | 理学部2号館 2-10 | 011-706-3558 |
| 学生居室2 | 理学部2号館 2-05 | 011-706-3583 |
| Jマテ実験室1 | 理学部2号館 1-07 | 011-706-3500 |
| Jマテ実験室2(試料切削室) | 理学部2号館 1-05 | |
| Jマテ実験室3(試料作成室) | 理学部5号館 1-10 | 011-706-3500 |
| 網塚教官室 | 理学部5号館 1-32 | 011-706-3484 |
| 柳澤教官室 | 理学部5号館 1-30 | 011-706-4422 |
札幌駅から研究室までの道のり
重い電子系超伝導体UPt3 の極低温磁化測定
セリウムやウラン含む金属化合物の中には、電子が通常の金属の電子の100~1000倍の質量を持っているように見える物質があり、これらの物質は「重い電子系化合物」と呼ばれています。この重い電子系化合物は、低温で比熱や磁化率が大きく、多くの場合、強磁性や反強磁性というような様々な磁性を示します。これらの重い電子の起源は4f、5f電子による強いクーロン斥力にあると考えられていますが、この重い電子系化合物の中には、さらに低温で(強いクーロン斥力にもかかわらず)電子がクーパー対をつくり、超伝導になるものがあります。この超伝導は通常の(BCSタイプの)超伝導とは性質が異なる「異方的超伝導」となります。この異方的超伝導体の一例として、「スピン三重項超伝導体」や「多重超伝導相」などが挙げられます。通常の超伝導体では、上向きスピンを持つ電子と下向きスピンを持つ電子からクーパー対が形成されます(スピン一重項超伝導体)。磁化率が大きい物質の場合、非常に強い磁場中ではスピンが揃うほうがエネルギー的に安定となるので、磁場中ではスピンを揃えようとする効果と超伝導との競合(常磁性効果)が起こります。このため、超伝導が破れる磁場(上部臨界磁場、Hc2)が低温で抑制されたり、超伝導状態での熱平衡磁化曲線が上部臨界磁場で切り立った形になります。一方、スピン三重項の超伝導体では、同じ向きのスピンがクーパー対をつくるため、磁場方向とスピン方向が同じ場合、常磁性効果は起こりません。
UPt3は典型的な重い電子系超伝導体のひとつです。この超伝導体は、低温低磁場相(A相)、低温高磁場相(B相)、高温相(C相)といった3つの異なる超伝導状態をもつ異方的超伝導体です。その熱平衡磁化曲線の超伝導成分を図1に示します(この磁化曲線は私達が独自に開発したキャパシタンス式ファラデー磁力計で測定しました)。内挿図には全体の磁化曲線が示されています。白矢印で示した磁場でB相からC相への相転移に伴う磁化の「折れ」が見られます(私達のグループが磁化曲線のこのような異常を初めて発見しました)。また、黒矢印の磁場(Hc2)で超伝導が壊れます。常磁性磁化率が小さい六方晶c軸方向の磁化曲線(図中でH//cと示されています)は、Hc2直下で非常に切り立った形をしているのに対し、常磁性磁化率が大きいc面方向の超伝導磁化曲線(図中で H⊥c と示されています)はそのような振る舞いが見られず、なめらかです。この様な振る舞いはスピン一重項超伝導体では起こり得ず、UPt3がスピン三重項の超伝導体であることがわかります。

図1 キャパシタンス式ファラデー磁力計を用いた極低温精密磁化測定によって得られたUPt3単結晶の熱平衡磁化曲線の超伝導成分
[TOPICS] URu2Si2 における隠れた秩序と微弱反強磁性
URu2Si2 は、17.5 K(= To) でウランの5f 電子による2 次相転移を示し、約1.2 K(= Tc)で異方的超伝導状態に転移する重い電子系超伝導体です。このTo における相転移で5f 電子のどんな自由度が凍結しているのか(= 秩序変数は何か)という問題は、重い電子系分野で長年解けていない問題の一つとして注目されています。この物質は、1985-6年にドイツ・オランダ・アメリカのグループによって独立に発見されました[1-3]。1987 年に最初の中性子散乱実験が行われ [4]、 Toより低温で反強磁性秩序の発達が観測されたことから、磁性と超伝導が共存する系として注目を集めました。しかし、AF相の秩序磁気モーメントの大きさ(μord)はわずか 0.03 μB(ボーア磁子)程度と極めて小さく、転移に伴うエントロピー変化量と単純には対応しません。さらに、AF 秩序で期待される内部磁場がSi 核 NMR やμSR 測定では観測されない、という奇妙な点があり、弱い反強磁性が相転移の本質かどうかが問題となっていました。これらの実験事実を説明するために様々な理論的アイデアが提案されてきましたが、それらは、弱い反強磁性を本質と考える立場と副次的現象ととらえる立場の二つに大きく分かれます。前者では秩序変数は f 電子のスピンであり、g 因子が量子揺らぎ等により抑制される機構が議論され、後者では、未だ観測にかからない反強四極子秩序[5]などの「隠れた秩序」の存在が提案されてきました。この問題に対し私達は最近、圧力に対するAF相の応答を中性子・NMR・μSRを用いて調べ、AF相の起源について次のような新しい事実を明らかにしました。
先ず、静水圧下中性子散乱実験(P < 2.8 GPa)を原研・阪大・Leiden大との共同研究として行いました[6]。その結果、加圧に伴い反強磁性による中性子のBragg散乱強度が著しく増強される振る舞いを見つけ、AF相を調べる上で圧力が有効なパラメータであることがわかりました(図1)。約1 GPaの加圧によってμordは 0.02 mB/U から0.25 μB/U へと連続的に変化し、さらに Pc ~ 1.5 GPaで 0.4 μB/Uへと急激に増大します。Pc より高圧では、系は3D-Ising 型反強磁性体として振る舞うことがわかりました。

図1 静水圧下中性子散乱実験によって得られたURu2Si2単結晶の反強磁性モーメントμordの温度・圧力変化。(反強磁性が試料に一様であると仮定して求めている)
この実験とほぼ並行して、松田和之氏(都立大)らが静水圧下29Si-NMR測定を行い、圧力誘起反強磁性に伴う共鳴線の分裂を発見しました [7]。しかし、観測された分裂は「部分的」であり、常磁性状態で存在する共鳴線が反強磁性発生後も有限値をとって残ることがわかりました。さらに、AFの発生により分裂した共鳴線は、その強度が加圧で増加するのに対し、共鳴周波数は殆ど圧力に依存しません。この結果から、AF相は試料内に不均一に発生していること、そして、中性子散乱強度の変化は、μord ではなくAF相の体積率 VAF の増大を見ていたに過ぎないことが明らかとなりました。
NMR測定の最低圧は0.3 GPaでしたが、圧力下における両実験結果の対応から、常圧下における VAF の値は僅か1% 弱と見積ることができます。これは通常のNMRやμSRの分解能では観測できない大きさです。すなわち、中性子散乱によってのみ観測される弱い反強磁性の本質は、試料内の微少領域で発生する反強磁性の「島」であることがこれらの実験結果より強く示唆されます。(ごく最近、松田氏らはさらに精度を高めた実験を行い、常圧においても反強磁性の共鳴ピークが存在することを確かめています[8]) また、このことは同時に、試料の99% 以上を占め、比熱に大きな異常をもたらす「隠れた秩序」がこの系に確かに存在することを意味しています。
この隠れた秩序と反強磁性の競合状態を更に詳しく調べるために、静水圧下μSR 実験をスイス・ポールシェラー研究所(PSI)で行いました[9]。金属に対する NMR 実験では試料表面近傍の性質しか観測できず、また、試料を粉末化するため歪みによる影響を受ける恐れがあります。その点、μSRは単結晶内部を輪切りにして(しかもゼロ磁場で)観測できるという利点があります。実験の結果、AF相の圧力誘起に顕著な試料依存性があることを確かめました。μSRスペクトルの初期アシンメトリーおよび回転周波数の圧力・温度依存性に対する詳しい解析から、この系では、両秩序相が同程度の凝縮エネルギー(To ~ 17.5 K; TN ~ 20K)を持ってほぼ縮退し、試料の熱処理や加圧で起こる微視的環境の変化によって1次転移していることがわかりました(図2、図3)。私達はさらに1軸応力を用いた詳しい実験から、この不均一磁性発現の引き金となる物理量として、軸性格子歪みc/aが重要であろうと考えています。[10]

図2 静水圧下ゼロ磁場ミュオンスピン緩和測定によって得られたURu2Si2単結晶(as grown)における反強磁性体積率および自発的ミュオンスピン回転周波数の温度・圧力変化。

図3 NMRおよびμSR測定によって得られた異なるURu2Si2試料に対する反強磁性体積率の圧力変化の比較
以上、高圧下における三つの微視的磁気測定結果に基づくと、URu2Si2では、基本的には隠れた秩序と超伝導の2相が競合もしくは共存しており、そこに僅かな歪みの影響によって反強磁性相が1次相転移で不均一に誘起される、という描像を描くことができます。「弱い反強磁性は本質か」という15年来停滞していた議論に対する答えを得たことは、この系の理解に対するひとつの大きな前進といえるでしょう。しかし、このような磁性-非磁性相分離状態がどのような形態をとって広い圧力-温度領域で安定に存在しうるのか、まだわかよくわかっていません。また、肝心の隠れた秩序の本質はなにか、また超伝導とはどのような関係にあるのか、という問題は依然として解けておらず、さらに詳しい研究を進めているところです。
ここにあげた研究は、以下の方々との共同研究です: 目時直人氏(原研先端研)、佐藤真直氏(SPring-8/JASRI)、河原崎修三教授(阪大理)、渡邊健二氏(阪大理)、都福仁教授(阪大理)、吉沢英樹教授(東大物性研)、髭本亘氏(高エ研物構研)、永嶺謙忠教授(高エ研物構研)、Dr. D. Andreica(ETH Zurich, UBB)、Prof. A. Schenck(ETH Zurich)、Prof. F.N. Gygax(ETH Zurich)、Dr. A. Amato(PSI)、松田和之氏(都立大理)、小堀洋教授(千葉大理)、小原孝夫教授(姫路工大理)、Prof. J.A. Modish(Leiden大)、Dr. Huang Ying Kai(Amsuerdam大)、桑原慶太郎氏(都立大理)、横山淳氏(茨城大理)、天谷健一氏(北大理)、野崎順氏(北大理)、宮崎志功氏(北大理)、伊藤征一朗氏(北大理)。
参照文献
[1] T.T.M. Palstra et al., Phys. Rev. Lett. 55 (1985) 2727.
[2] W. Schlabitz et al., Z. Phys. B 62 (1986) 171.
[3] M.B. Maple et al., Phys. Rev. Lett. 56 (1986) 185.
[4] C. Broholm et al., Phys. Rev. Lett. 58 (1987) 1467.
[5] F.J. Ohkawa and H. Shimizu, J. Phys.: Condens. Matter 11 (1999) L519.
[6] H. Amitsuka et al., Phys. Rev. Lett. 83 (1999) 5114; J. Phys. Soc. Jpn. 69 (2000) suppl. A. 5.
[7] K. Matsuda et al., Phys. Rev. Lett. 87 (2001) 87203; Physica B 312-313 (2002) 504.
[8] K. Matsuda et al., J. Phys.: Condens. Matter 15 (2003) 2363.
[9] H. Amitsuka et al., Physica B 326 (2003) 418.
[10] M. Yokoyama et al., J. Phys. Soc. Jpn. 71 (2002) Suppl. 264; Ph.D. Thesis, Hokkaido University, 2003.
[TOPICS] カゴ状化合物のラットリングとトンネリング
T. Yanagisawa et al.: J. Phys. Soc. Jpn. 80 (2011) 043601.
T. Yanagisawa et al.: J. Phys. Soc. Jpn. 77 (2008) 074607.
1.研究の背景
まずは、図1をごらんください。左側に見えるのは幼児や猫が遊ぶ「ガラガラ」(英語では"Rattler" ラトラー)と呼ばれるおもちゃです。カゴ状の容器の中に鈴やボールが内包されています。「ラットリング」とは「ガラガラと音を鳴らす」という意味の英単語です。ガラガラ蛇のことも英語では"Rattle Snake"と呼びますね。
右にも似たようなカゴがあります。こちらは原子のカゴです。このようなカゴ状の結晶構造を持つ化合物は数多く知られています。原子のカゴの大きさはたかだか数ナノメートル(~0.000000001 m)。結晶の中においてはこれらの原子のカゴは規則的に並んでいます。原子のカゴの中をよく見ると、1つの原子が内包されています。図1の右に示した三つの物質に於いては、この内包原子が中心から外れた位置(オフセンター位置)を運動していると考えられています。このミクロな原子のガラガラ運動も、左のガラガラおもちゃと類推して「ラットリング」と呼びます。
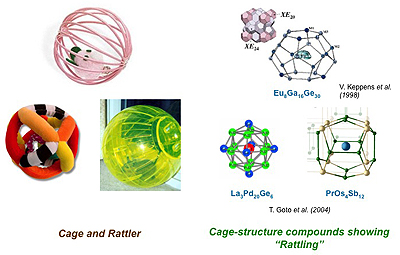
図1 幼児や猫が遊ぶ玩具「ガラガラ」(左)と内包イオンを持つ原子のカゴ(右)
図1の右下にあるPrOs4Sb12という物質は、充填スクッテルダイト化合物と呼ばれる物質で、ラットリングを示すカゴ状化合物です。Os(オスミウム)原子が4つとSb(アンチモン)原子12個から構成されるカゴの中に、希土類元素(レアアース)のPr (プラセオディウム)原子(金属化合物なので正確にはイオン)が内包されています。2004年に後藤(新潟大)らよってPrOs4Sb12のラットリングが観測されて以来、原子カゴに内包された希土類イオンの局所振動と、電子系との強相関によって生じる局所電荷ゆらぎがもたらすエキゾチックな物性が注目され、カゴ状化合物を対象に「ラットリング」をキーワードにした研究の扉が開かれました。[1] それ以前にもMaple(UC San Diego)らによってPr化合物で初の重い電子超伝導、磁場誘起四極子秩序など多彩な物性を示すことが報告され非常に注目されてきた物質です。[2] また、充填スクッテルダイト化合物の物質群 RT4X12 (R = 希土類, T = Fe, Ru, Os, X = P, As, Sb)は、文部科学省の特定領域研究「充填スクッテルダイト構造に創出する新しい量子多電子状態の展開」によって日本国内で精力的に研究が推進されてきました.以上の研究背景を鑑み、我々はPrOs4Sb12のラットリングに起因するエキゾチックな物性を探索するために類似物質NdOs4Sb12を研究ターゲットに選びました。次に結晶構造を詳しくみてみましょう。
この記事には続きがあります:続きを読む ...
微視的測定
基礎物性を北大で調べた後、さらに微視的な情報を必要とする場合、狙いを絞って中性子散乱、ミュオン スピン回転・緩和・共鳴(muSR)などの測定を、高エネルギー加速器 研究機構(つくば)、日本原子力研究所(東海)、Paul Scherrer 研究所(ス イス)等に出向いて行っています。中性子散乱実験

研究用原子炉JRR-3M
共鳴X線散乱実験
ミュオンスピン回転・緩和・共鳴(muSR)実験

高エネルギー加速器研究機構(KEK)
にあるミュオンポート
ミュオンスピン回転・緩和・共鳴(muSR)実験
プラスの電荷とスピンを持った正ミュオンは、固体中に打ち込まれると、数ナノ秒のうちにスピンの向きをそろえて格子間位置に止まります。その位置に磁場があると、ミュオンはその回りを歳差運動し、2.2マイクロ秒の寿命でスピンの向きに陽電子を放出して死滅します。この陽電子の時間・空間分布を通じてミュオンの運動を調べることにより、物質内部の磁場の分布や変化に関する情報を得ることができます。私達のグループでは、年に1~2度、高エネルギー加速器研究機構(KEK)やポールシェラー研究所(PSI)でこの実験を行っています。
高エネルギー加速器研究機構(KEK) |
汎スイス、ポールシェラー研究所 |
実験風景1 |
実験風景2 |
実験を終えて |
スイスからドイツへ向かう寝台特急の朝 |
中性子散乱実験
中性子は電荷を持たずにスピンを持つ粒子です。微小磁石としての性質があり、これを物質に打ち込むと、物質中の電子磁気モーメントや原子核と力を及ぼし合って散乱されます。中性子散乱実験では、中性子の波としての性質である回折現象を利用し、物質中の磁気モーメントの配列や運動を調べることができます。私達のグループでは、年に 3~4 回、東大物性研究所の共同利用として日本原子力研究所で実験を行っています。
研究用原子炉JRR-3M |
汎用三軸型中性子分光器 |
実験風景 |
実験終了後の反省会 |
[Method] キャパシタンス式磁力計を用いた極低温精密磁化測定
低温で磁化を測定する方法としては、試料をピックアップコイルの中で動かして誘導起電力を測る誘導法と試料に交流磁場をかけて応答をみる交流法が、これまで主に用いられてきました。しかし、これらの方法では摩擦や誘導電流による発熱があるため、1 K以下の極低温下で精密な測定を行うことは非常に困難でした。私たちのグループでは、榊原教授(現、東大物性研教授)、卒業生の田山孝氏(現、東大物性研助手)らが中心となって独自の磁力計を開発し、希釈冷凍機温度領域(40 mK ~ 5 K)で9万エルステッド(参考までに、地磁気の大きさは0.1エルステッド以下)までの磁場掃引による高感度磁化測定を可能にしました。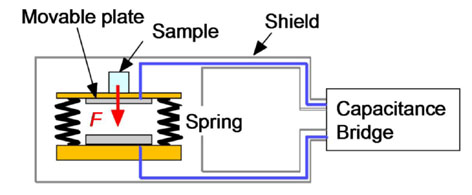
キャパシタンス式磁力計の動作原理図
この磁力計は、磁性体に働く力が磁化と磁場勾配に比例することを利用したものです。磁性体に働く力に比例して平行平板コンデンサー(電極間距離約 0.1 mm)の可動電極が動き、静電容量が変化するので、この静電容量を高精度キャパシタンスブリッジで正確に測ることによって磁化がわかるという仕組みです。つまり、下図のようなキャパシタンス式の「バネばかり」で磁性体に働く力を測定しているのです。試料をほとんど動かす必要が無いので発熱が無いことが、極低温領域での静的磁化測定を可能にした理由です。この装置の開発により、たとえば、重い電子系の異方的超伝導状態における熱平衡磁化の振る舞いを初めて明らかにすることができました。私達は現在、静水圧下および1軸応力下で磁化測定を可能にするため、さらに装置の機能を拡張しています。
キャパシタンスセル |
圧力セル搭載型改良キャパシタンスセル |
極低温磁化測定システムを組み込んだ |
断熱セル内部 |
物質合成
プラズマ炉、3極および4極アーク炉、アニール炉などを用い、金属間化合物の合成と単結晶化を行います。テトラアーク炉
プラズマジェット炉
放電加工機
物質評価(X線構造解析・EPMA等)
4極(テトラ)アーク炉外観 |
ベルジャー部 |
単結晶が成長する様子 |
引き上げられた単結晶の例 |
高温大気炉 |
シリコニット炉 |
テトラアーク炉
プラズマ炉、3極および4極アーク炉、アニール炉などを用い、金属間化合物の合成と単結晶化を行います。テトラアーク炉
プラズマジェット炉
放電加工機
物質評価(X線構造解析・EPMA等)
4極(テトラ)アーク炉外観 |
ベルジャー部 |
単結晶が成長する様子 |
引き上げられた単結晶の例 |
高温大気炉 |
シリコニット炉 |
[TOPICS] 重い電子系超伝導体UBe13の超伝導混合状態における磁気特性
1911年にカマリン・オンネスによって発見された超伝導現象に関する理解は、1957年のBCS(Bardeen-Cooer-Schrieffer)理論の提唱により、ほとんど解決したかに思われました。しかし、1980年代になると、セリウムやウランを含む重い電子系化合物による超伝導や、有機超伝導、高温超伝導の発見(1986年)をきっかけに、BCS理論では説明できない、いわゆる『非BCS超伝導体』が次々と発見されるようになりました。これらの非BCS超伝導体は、上記のような重い電子系化合物 をはじめとする強い電子相関を持つ系、すなわち『強相関電子系』において多く見られ、『異方的超伝導ギャップ』や『多重超伝導相』、BCS理論では説明不可能な『異常な上部臨界磁場Hc2』、さらには『磁性と超伝導の共存』など、数多くの興味深い現象を示します。特に、『磁性と超伝導の共存』は、本来水と油のような関係であると考えられてきた『磁性』と『超伝導』という物理現象を結びつけるという意味で、これまでの常識を覆すものです。
これらの非BCS超伝導を研究する上での、根本的課題の一つは『強い斥力がはたらくはずのこれらの強相関電子系においてなぜ超伝導が起こるのか?』ということです。超伝導現象は、ある電子と別の電子が引かれ合って対を成し(Cooper対)、そのような電子対を物質中の巨視的な数の電子が一斉に形成するというような一種のボーズ凝縮のようなものとして解釈できます。これは微視的には、ボーズ粒子としての何らかの『量子ゆらぎ』がフェルミ粒子である電子同士間にはたらき、相互作用することで電子対を形成するという解釈がなされます。BCS理論で説明可能な従来型の超伝導体の多くは格子振動、つまり「フォノン」を媒介としたものであると考えられています。電子は当然のことながら電荷を持ちますから、電子同士にはクーロン斥力がはたらきます。つまり超伝導になるにはクーロン斥力に打ち勝つだけの『引力』が必要ということになります。私たちの研究室で取り組んでいるセリウムCeやウランUを含む重い電子系物質では、4f, 5f電子が主な物性を担っており、それらの物質中の電子は通常の金属において伝導を担うs, p電子に比べ、相当に大きなクーロン斥力を感じていると考えられます。これらの電子相関の強い系おいて通常のBCS超伝導が実現するのは難しいと考えられています。なぜなら、フォノンを媒介としたBCS超伝導が起こるためには、電子同士がかなり近づく必要があるからです。(厳密には片方の電子からもう片方の電子を相対的にみたときの電子の存在確率はデルタ関数的であり、距離が同じところの存在確率が最も大きくなります)それにも関わらず、なぜ重い電子系化合物には超伝導を示すものがあるのでしょうか?言い換えれば、『重い電子系超伝導体をもたらす量子揺らぎ』は何なのでしょうか?
重い電子系化合物に超伝導をもたらす起源の可能性のひとつとして量子臨界点の存在が挙げられます。重い電子系化合物には、低温において反強磁性秩序や強磁性秩序、さらには多極子秩序といった多彩な秩序状態を示すものが多くあります。そして、それらの秩序-無秩序転移温度は圧力や元素置換などによって絶対零度近傍に制御することが可能です。こうして得られた秩序-無秩序転移温度が絶対零度に落ち込む点は『量子臨界点』とよばれます。この量子臨界点近傍では、熱揺らぎは押さえられ、電子系における量子揺らぎのはたらきが顕著になります。そして、最近の研究から、それらの量子揺らぎが超伝導の引力に起因しているのではないかと考えられるようになりました。たとえば、反強磁性を示す物質であれば、反強磁性揺らぎが超伝導を導く要因になっているのではないか、と考えるわけです。実際に、重い電子系反強磁性体における量子臨界点近傍において非BCS超伝導が発見されている例が最近では多く見つかっています。
このようなエキゾチックな超伝導の起源をさらに深く探るにはどうしたらよいのでしょうか?反強磁性体における超伝導を例にとって考えてみましょう。それらの物質においてはその量子臨界点近傍で反強磁性ゆらぎが強いわけですから、Cooper対を形成しようする電子同士においても反強磁性的な相互作用、つまりスピンを反平行向きにしようとする相互作用がはたらきます。したがって、反平行スピンをもつCooper対が形成されやすいということになります。このような反平行スピンからなるCooper対をもつ超伝導は、スピン一重項(spin-singlet pairing)超伝導とよばれます。同様に、平行スピンをもつCooper対からなる超伝導はスピン三重項(spin-triplet pairing)とよばれます。電子対波動関数を考えるとき、全体の波動関数は単純にはスピン部分と軌道部分の積から成り立ちます。電子はフェルミ粒子ですので、Cooper対の電子対波動関数は粒子の入れ替えに対し反対称であることが要請されます。電子対のスピンが平行であるとするとスピン部分の波動関数は粒子の入れ替えに対して対称であるため、軌道部分の波動関数は反対称(奇パリティ:p波やf波)となります。一方で、反平行スピンについては、軌道部分の波動関数は粒子の入れ替えに対して対称なもの(偶パリティ :s波やd波)になります。また、物質中では原子は結晶を成しているため、その結晶場中における引力相互作用も物質の対称性を反映したものになるはずであり、軌道部分の波動関数はその引力相互作用の対称性を反映します。つまり異方的な引力相互作用が異方的超伝導ギャップとして超伝導ギャップの対称性に反映されます。したがって、Cooper対のパリティがsingletであるかtripletであるかということや、電子対の軌道部分の波動関数がどのようなものであるか、ということは超伝導の起源を探るために非常に重要な情報だということが言えます。
私たちの研究室では特に、5f電子をもつウラン系の重い電子系超伝導体における超伝導メカニズムに興味を持ち、その超伝導対称性を明らかにすることを目的としていろいろな物性測定からアプローチしています。
本研究室が取り組んでいるUBe13もウラン系非BCS重い電子系超伝導体の一つです。UBe13は立方晶の結晶構造をもち、低温で通常の金属よりも遥かに大きな電子比熱係数を示す重い電子系化合物ですが、1983年にスイスのOttらによって このUBe13が超伝導状態を示すことが発見されました[1]。超伝導転移温度以下の比熱の温度依存性がT3的で3Heにおけるスピン三重項p波超流動状態で実現しているとされているABM (Anderson-Brinkman-Morel) 状態のものに類似していることから、UBe13においてもスピン三重項が実現しているのではないかと提唱され、ウラン系化合物における最初の異方的超伝導として一躍脚光を浴びました [2]。また、NMR(Nuclear-Magnetic-Resonance)スピン格子緩和率 [3]、磁場侵入長 [4]、さらには超音波吸収 [5] の温度依存性からも、超伝導ギャップが点(ポイントノード)または線(ラインノード)でゼロになるような異方的超伝導ギャップを示唆するということが報告されました。しかし、結局のところ、これらの結果を総合して見てみても、超伝導ギャップがどのような対称性を持っているのかについて、今のところ決着はついていません。また、超伝導のパリティを決定する上で重要な微視的なスピン帯磁率の結果においても、現在のところNMR Knightシフトの結果とmuon-SR Knight shiftの結果は一致していません。つまり、超伝導対がスピン一 重項なのか、それともスピン三重項なのかさえはっきりしていないというのが現状です。このように、発見から既に四半世紀以上も経過した現在もなお、UBe13の超伝導はその超伝導対称性が明らかになっていないだけではなく、その他の多くの未解決な問題を抱えています。本研究室では、UBe13における超伝導対称性とその風変わりな超伝導の性質を解明するため、最近原子力機構先端研の芳賀芳範教授が作成に成功した純良な試料を用い、超伝導状態における極低温DC磁化測定をはじめ、磁場中比熱測定など多方面からのアプローチを行っています。
参考文献
[1] H. R. Ott et al., Phys. Rev. Lett. vol. 50 (1983) 1595.
[2] H. R. Ott et al., Phys. Rev. Lett. vol. 52 (1984) 1915.
[3] D. E. MacLaughlin et al., Phys. Rev. Lett. vol. 53 (1984) 1833.
[4] D. Einzel et al., Phys. Rev. Lett. vol. 56 (1986) 2513.
[5] B. Golding et al., Phys. Rev. Lett. vol. 55 (1985) 2479.
[Method] 超高圧における物性研究
関連項目
インデンターセルによる高圧下電気抵抗・AC磁化測定
MPMS用インデンター&ピストンシリンダセルによる静水圧下DC磁化測定
ピストンシリンダセル断熱法比熱測定
極限科学には歴史的、思想的な背景がある。それは人間性の本質そのものに根源を持っている。一言でいえば、未知なものに一歩踏み込んでそれを知ろうとする好奇心である。(伊達宗行:極限の科学(講談社))
モノを極限環境においたとき、普段の常識では考えられない変化をすることがあります。例えば、酸素が金属になりその果てには超伝導を起こしたり、シリコンのような良く知られた絶縁体が金属になったりします。ここで極限環境とは極低温・強磁場・超高圧、もしくはこれらを組み合わせた複合状態のことを指します。私たちの研究グループでは、強相関電子系と呼ばれる物質群を極限環境下におくことで、新奇な相転移現象(例えば圧力誘起超伝導)の探索などを行っています。

図1
ここでは簡単に高圧発生装置について紹介します。図 2 にいくつかの高圧セルの特徴をまとめています。一般に高い圧力を発生させるには試料空間の大きさが犠牲となり、目的に応じて装置を使い分けることになります。最も広く使われているのは「ピストンシリンダーセル」であり、最大発生圧力は約2.5 GPa(25000気圧)です。この装置は、試料空間が大きいためほとんどの物性測定が可能なことがメリットです。私たちの研究グループでも様々な測定に使用しています。(下記参照)一方で、最大発生圧力の観点では他の追随を許さないのが「ダイヤモンドアンビルセル」です。この装置は試料空間が極端に狭いためバルク測定が困難であるし、取り扱いも非常に難しいのですが、その達成圧力は100 GPa(百万気圧!)を超えます。現在では地球の中心の圧力(360 GPa)に近い高圧力が研究室単位でも実現できるようになり、地球科学の分野でも応用されたりしています。残念ながら現在、我々の研究グループでは使用しておりませんが、将来的な導入を検討しています。
図2
私たちの研究グループで行っている高圧実験の最大の特徴は「インデンターセル」と呼ばれている高圧セルを用いていることです。これは岡山大学小林教授のグループで開発された特殊な圧力セルで、特徴としては
1. ピストンシリンダー以上の高圧発生可能 (最大5 GPa(50000気圧))
2. 精密磁気測定に可能な試料空間を確保
3. 小型であるために希釈冷凍機やPPMSに取り付け可能
などが挙げられます。現在、インデンターセルを用いた研究が可能なのは私たちのグループを含めても世界で数グループしかありません。
MPMS用ピストンシリンダーによる高圧下DC磁化測定
ドイツ・Braunschbeing工科大学Stefan Su(ウムラウト)llow 教授らによって開発されたDC磁化測定用の単層式ピストンシリンダーセル(Cu-Be合金製)です。市販のSQUID磁力計(MPMS, Quantum Design社)に取り付け可能となっており,理想的なSQUID電圧波形が得られるように非常に細長い構造になっています(全長~150 mm)。温度は2 K、圧力は約1 GPa(10000気圧)までの測定が可能です。
図1 MPMS用ピストンシリンダーセル概観
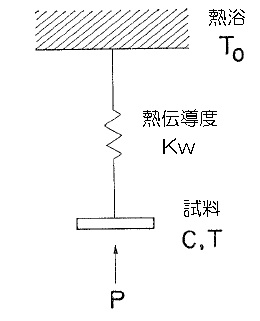
緩和法比熱測定
熱緩和法とは、試料に与えていた熱を切った際の試料温度の緩和現象から比熱を求める実験手法です。具体的には、試料の回りに精密に温度コントロール可能な熱浴T0を作り、試料と熱浴との間を比較的弱い熱伝導パス(熱伝導度KW)で結びます。(図1)試料部には小型の温度計とヒーターを装着し、このヒーターに通電する事で試料温度を熱浴よりΔT だけ高い定常状態で保持しておきます。その後、一気にヒーターを切ると熱伝導パスを通じて試料から熱浴に熱が逃げて行きます。この温度緩和過程は通常指数関数型になり、その時定数を解析する事により試料部の比熱を求めます。 この実験手法により、わずか数mg程度の小さな試料の比熱を広い温度範囲かつ強磁場中で測る事が出来ます。比熱からは物質のエントロピーを見積もる事ができて、系のもつ微視的自由度の振る舞いを予想できます。比熱は物質の性質を理解する上で最も重要な物理量のひとつです。我々の研究室では、Heliox :0.36 [K] < T < 200 [K] 、 B < 12 [T] (図2)
PPMS :2 [K] < T < 380 [K] 、 B < 9 [T] (図3)
これらの装置により比熱測定を行っています。図4にPPMSでの実際の測定結果を示します。
図1 |
図2 |
図3 |
図4 |
放電加工機
金属ワイヤーに電気を通し、試料を溶かしながら正確に平面を出すことで、試料の整形を行うことができます。 試料の切断は油の中で行われ、放電による過剰な発熱や、試料の切りくずが空気中に舞うことを防ぎます。よって、放射性物質でも安全に試料整形することができます。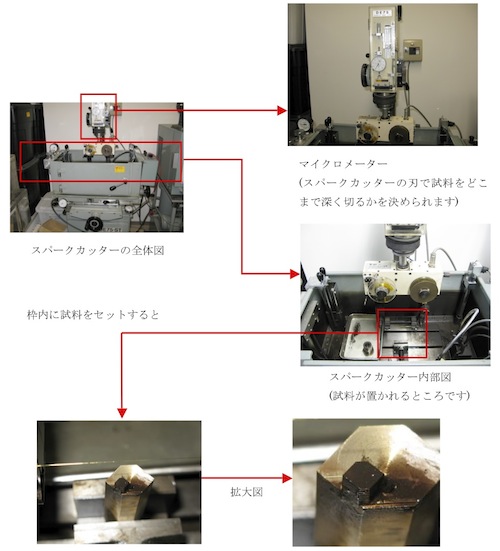
図1 実際にスパークカッターで試料を加工する過程
(軸方向はX線ラウエ法などで決定している)
SQUID磁束計による磁化測定

図1 Quantum Design社製MPMS
Quantum Design社製のMPMS(Magnetic property Measurement System) (図1) は取り扱いが簡便で測定感度が高い磁化測定装置です。 この装置は引き抜き法と呼ばれる方法を用いて磁化を求めています。引き抜き法とは図2のようなコイルの中で磁化した試料を引き抜きコイルに発生した誘導起電力を測定、フィッティングすることで磁化を求める方法です。コイルが上下と中心で逆向きになっていることで外部の磁場の干渉やノイズを除去することができます。 MPMSで測定できる温度は2~400 K、印加できる磁場は-5.5 T~5.5 Tです。また圧力セルを用いることで高圧下での磁化測定、回転機構を用いることで角度分解磁化測定といった測定も可能になります。|
図2 引き抜き法の概念図 |
図3 試料の位置に対する誘導起電力とフィッティング関数 |
MPMS用インデンターセルによる静水圧下DC磁化測定
図1のMPMS用インデンターセルを用いることで高圧下(~3 GPa)DC磁化測定を行うことができます。
図1 MPMS用インデンターセル
試料を圧力セルに入れて測定すると、試料の磁化とBack Ground である圧力セルの磁化を足した磁化が測定されます。そこで試料のみの磁化を得るためには一般的に図2のようにBack Groundの磁化を差し引く方法が用いられます。MPMSは電圧波形をフィットして磁化を求めていますが圧力セルを測定した時の電圧波形は図3のように高温で乱れてしまいます。フィットして磁化を正確に求めることがでないので、図2の方法では高温における試料の磁化を求めることができません。
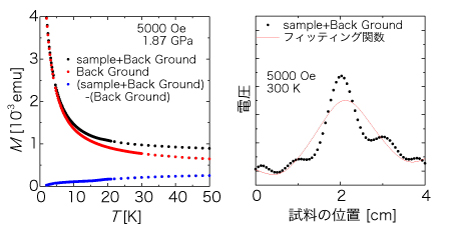
図2 磁化の差し引きの様子 図3 試料と圧力セルの高温での電圧波形
そこで私たちの研究室では図4のように電圧波形の段階で差し引きを行い、それをフィットして磁化を求めています。この方法を用いれば電圧波形の乱れる高温でも上手くフィットでき磁化を正確に求めることが可能になります。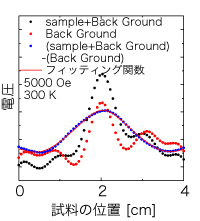
図4 電圧波形の差し引きの様子
図5はMPMS用インデンターセルと電圧波形の差し引きを用いて測定したURu2Si2の高圧下における磁化率の温度依存性です。この試料に対しては報告例のない最大圧力1.87 GPaの精密磁化測定に成功しています。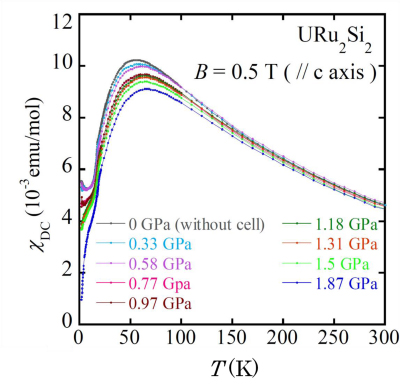
図5 URu2Si2の高圧下における磁化率の温度依存性
ピストンシリンダーによる高圧下電気抵抗・AC磁化率測定
ハイブリッド型ピストンシリンダーセル(Ni-Cr-Al合金とCu-Be合金の二層構造)を用いて、最大2.5 GPa(25000気圧)までの電気抵抗率・交流帯磁率などのバルク測定が可能です。試料空間が大きいため感度のよい測定が行えるのが特徴です。コンパクトなサイズのため、PPMSや希釈冷凍機などに取り付け可能です。
図1 ピストンシリンダーセル概観
X線を用いた物質評価
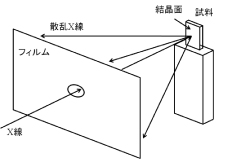
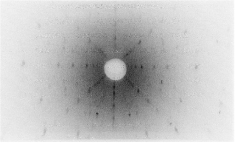
アーク炉やプラズマジェット炉で作製した試料をX線を用いて評価します。評価の手法はラウエ法、粉末ディフラクトメーター法、EPMA(Electron Probe Micro Analyzer)です。 ・ラウエ法 図1のようにX線を単結晶試料に当てて、散乱したX線でフィルムを感光させます。このときブラッグの反射条件を満たしてX線が強めあうと図2のように黒い斑点がフィルムに現れます。この斑点の対称性(4回対称、鏡映面等)は結晶の対称性を反映しているので結晶面の対称性、軸方向が分かります。|
図1 ラウエ法の概念図(背面反射法) |
図2 ラウエ写真の例 |
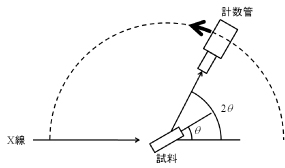
図3 粉末ディフラクトメーター法の概念図
・EPMA 試料に電子線を照射すると図5のような反応がおこります。この中の特性X線いうものは波長が原子によって決まっているX線です。電子線を照射したときに飛び出してくる特性X線の波長のスペクトルを調べることで電子線の当たった領域の構成元素と割合が分かります。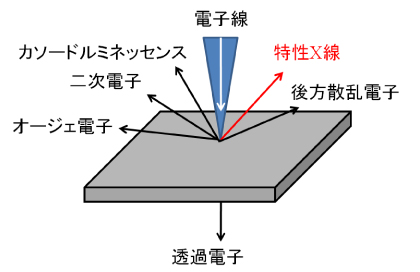
図4 電子線を試料に照射したときの反応
インデンターセルを用いた高圧下電気抵抗・交流帯磁率測定

図1 インデンターセル概観
インデンターセルの簡単な模式図を図2に示しています。中心に穴の開いたNi-Cr-Al合金製ブロック(hole piece)にあけた穴に液体の圧力媒体を満たし、先端部分に試料を取り付けたインデンター(NMWC:非磁性タングステン鋼)を差し込みます。この状態からプレス機で加圧することによって、hole pieceの穴を変形させて圧力を発生させる仕組みです。圧力はロックナットを締めることで保持しています。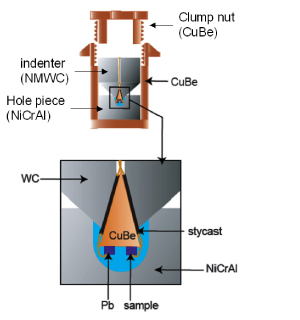
図2 インデンター型圧力セルの模式図
電気抵抗測定には4端子法を用いています。端子付にはスポット溶接や銀ぺーストなどをもちいています。(図3)非常に細かい作業のため写真のように顕微鏡を見ながらの作業となるため学生たちもはじめは苦労しますが 、一か月ほどで誰でもセッティングができるようになります。(図4)
|
図3 スポット溶接をしているところ |
図4 |
図6は私たちの研究室の学生が手作りした「巻き線機」です。手作り感たっぷりですが、1mm以下のコイルを非常に美しく巻くことができる優れモノです。
図5 インデンターセルに内蔵する微小コイル |
図6 ホームメイド「巻き線機」 |
Topics: Double ultrasonic dispersions due to rattling in SmOs4Sb12
|
Magnetic-Field-Independent Ultrasonic Dispersions due to Rattling in the Magnetically Robust
Heavy Fermion System SmOs4Sb12 Tatsuya YANAGISAWA, Yoichi IKEDA, Hitoshi SAITO, Hiroyuki HIDAKA, Hiroshi AMITSUKA, Koji ARAKI, Mitsuhiro AKATSU, Yuichi NEMOTO, Terutaka GOTO, Pei-Chun HO, Ryan E. BAUMBACH, and M. Brian MAPLE |
Elastic properties of the filled skutterudite compound SmOs4Sb12 have been investigated by ultrasonic measurements. The elastic constant C12(\omega) shows two ultrasonic dispersions at ∼15 K and ∼53 K for frequencies \omega between 33 and 316 MHz, which follow a Debye-type formula with Arrhenius-type temperature-dependent relaxation times, and remain unchanged even with applied magnetic fields up to 10 T. The corresponding activation energies were estimated to be E2 = 105 K and E1 = 409 K, respectively. The latter, E1, is the highest value reported so far in the Sb-based filled skutterudites. The presence of magnetically robust ultrasonic dispersions in SmOs4Sb12 implies a possibility that an emergence of a magnetically insensitive heavy fermion state in this system is associated with a novel local charge degree of freedom which causes the ultrasonic dispersion. J. Phys. Soc. Jpn. 80 (2011) 043601. (also available on cond-mat/1010.1387)
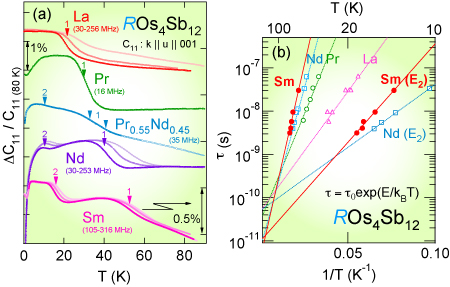
Figures (a) Comparison of the ultrasonic dispersions that appear in elastic constant C11 of ROs4Sb12 (R = La-Sm) at several frequencies. Lower arrowheads with numbers 1 and 2 indicate the relaxation point \omega\taui ∼ 1 for i = 1 and 2, respectively. (\omega is ultrasonic frequency and \tau is relaxation time) The displayed data have been shifted to eliminate overlapping with each other and the SmOs4Sb12 data are magnified three times for the \Delta C11/C11-axis. (b) Arrhenius plots of the characteristic parameters of the ultrasonic dispersions (Attempt time: \tau0(i), Activation Energy: Ei) for ROs4Sb12 (R = La-Sm). (*This research was performed at UC San Diego, Hokkaido University, and Niigata University in 2010.) |
Topics: Double ultrasonic dispersions due to rattling in SmOs4Sb12
|
Magnetic-Field-Independent Ultrasonic Dispersions due to Rattling in the Magnetically Robust
Heavy Fermion System SmOs4Sb12 Tatsuya YANAGISAWA, Yoichi IKEDA, Hitoshi SAITO, Hiroyuki HIDAKA, Hiroshi AMITSUKA, Koji ARAKI, Mitsuhiro AKATSU, Yuichi NEMOTO, Terutaka GOTO, Pei-Chun HO, Ryan E. BAUMBACH, and M. Brian MAPLE |
Elastic properties of the filled skutterudite compound SmOs4Sb12 have been investigated by ultrasonic measurements. The elastic constant C12(\omega) shows two ultrasonic dispersions at ∼15 K and ∼53 K for frequencies \omega between 33 and 316 MHz, which follow a Debye-type formula with Arrhenius-type temperature-dependent relaxation times, and remain unchanged even with applied magnetic fields up to 10 T. The corresponding activation energies were estimated to be E2 = 105 K and E1 = 409 K, respectively. The latter, E1, is the highest value reported so far in the Sb-based filled skutterudites. The presence of magnetically robust ultrasonic dispersions in SmOs4Sb12 implies a possibility that an emergence of a magnetically insensitive heavy fermion state in this system is associated with a novel local charge degree of freedom which causes the ultrasonic dispersion. J. Phys. Soc. Jpn. 80 (2011) 043601. (also available on cond-mat/1010.1387)
Figures (a) Comparison of the ultrasonic dispersions that appear in elastic constant C11 of ROs4Sb12 (R = La-Sm) at several frequencies. Lower arrowheads with numbers 1 and 2 indicate the relaxation point \omega\taui ∼ 1 for i = 1 and 2, respectively. (\omega is ultrasonic frequency and \tau is relaxation time) The displayed data have been shifted to eliminate overlapping with each other and the SmOs4Sb12 data are magnified three times for the \Delta C11/C11-axis. (b) Arrhenius plots of the characteristic parameters of the ultrasonic dispersions (Attempt time: \tau0(i), Activation Energy: Ei) for ROs4Sb12 (R = La-Sm). (*This research was performed at UC San Diego, Hokkaido University, and Niigata University in 2010.) |