我々は実験系の研究グループです。
物性物理学は多様な物質現象の中から新たな物理の基本法則を見つけ出すことを目指す学問です。
通常は熱散乱のベールに隠されている量子力学的な基底状態を、
極低温環境下における物性測定で詳らかにするべく、日々研究を続けています。
ここでは現在進行中の研究テーマと、実験手法・技術についてご紹介します。
研究内容
拡張多極子による動的応答
UNi4Bのトロイダル秩序状態における新しい電流誘起磁化現象
5f 電子系の磁性と超伝導
URu2Si2における隠れた秩序と微弱反強磁性
c-f混成によって誘発されるURu2Si2の格子不安定性(パルス強磁場下超音波測定)
重い電子系超伝導体UBe13の超伝導混合状態における磁気特性
112希薄系における局所的非フェルミ液体異常
4f 電子系の磁性と超伝導
単サイト四極子近藤効果の検証:
Y1-xPrxIr2Zn20 の弾性応答に観る 対数的温度変化
重い電子系超伝導体UPt3における極低温磁化測定
EuIn2P2における磁場中比熱測定
SmOs4Sb12 の静水圧力下超音波測定
磁場に鈍感な重い電子系スクッテルダイト化合物 SmOs4Sb12 のラットリング
(ラットリングを示す充填スクッテルダイト化合物の磁性と超伝導)
TmM2Si2(M: 遷移金属)系の磁性
非フェルミ液体的振る舞いを示す YbRh2Si2 の極低温磁性
研究手法/実験装置(一覧)
極低温基礎物性測定
キャパシタンス式極低温精密磁力計を用いた磁化測定(100μW希釈冷凍機)
SQUID磁束計による磁化測定、交流磁化率測定
緩和法比熱測定(HELIOX)
電気抵抗測定(Handmade希釈冷凍機)
高圧下物性測定
インデンターセルによる高圧下電気抵抗・AC磁化測定
MPMS用インデンター&ピストンシリンダセルによる静水圧下DC磁化測定
ピストンシリンダセル断熱法比熱測定
超音波物性測定
位相比較法(ヘテロダイン検波)を用いた弾性定数測定
蒸着装置&ネットワークアナライザ(超音波圧電素子制作)
微視的測定
中性子散乱実験
共鳴X線散乱実験
ミュオンスピン回転・緩和・共鳴(muSR)実験
物質合成
テトラアーク炉によるチョクラルスキー法単結晶試料育成
プラズマジェット炉による多結晶試料育成
フラックス法による単結晶試料育成
放電加工機
物質評価(X線構造解析・EPMA等)
放電加工機
金属ワイヤーに電気を通し、試料を溶かしながら正確に平面を出すことで、試料の整形を行うことができます。 試料の切断は油の中で行われ、放電による過剰な発熱や、試料の切りくずが空気中に舞うことを防ぎます。よって、放射性物質でも安全に試料整形することができます。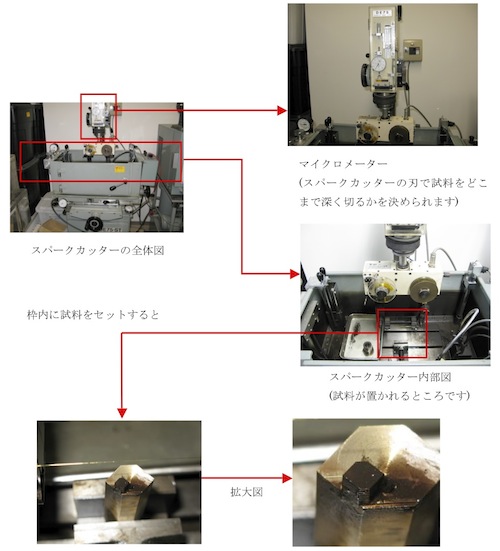
図1 実際にスパークカッターで試料を加工する過程
(軸方向はX線ラウエ法などで決定している)
MPMS用インデンターセルによる静水圧下DC磁化測定
図1のMPMS用インデンターセルを用いることで高圧下(~3 GPa)DC磁化測定を行うことができます。
図1 MPMS用インデンターセル
試料を圧力セルに入れて測定すると、試料の磁化とBack Ground である圧力セルの磁化を足した磁化が測定されます。そこで試料のみの磁化を得るためには一般的に図2のようにBack Groundの磁化を差し引く方法が用いられます。MPMSは電圧波形をフィットして磁化を求めていますが圧力セルを測定した時の電圧波形は図3のように高温で乱れてしまいます。フィットして磁化を正確に求めることがでないので、図2の方法では高温における試料の磁化を求めることができません。
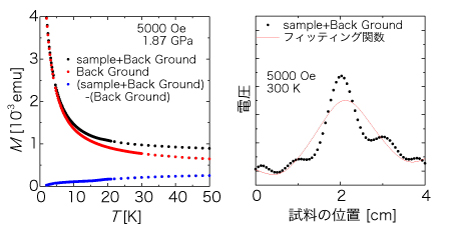
図2 磁化の差し引きの様子 図3 試料と圧力セルの高温での電圧波形
そこで私たちの研究室では図4のように電圧波形の段階で差し引きを行い、それをフィットして磁化を求めています。この方法を用いれば電圧波形の乱れる高温でも上手くフィットでき磁化を正確に求めることが可能になります。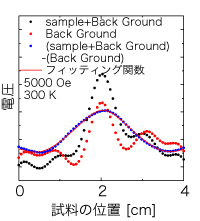
図4 電圧波形の差し引きの様子
図5はMPMS用インデンターセルと電圧波形の差し引きを用いて測定したURu2Si2の高圧下における磁化率の温度依存性です。この試料に対しては報告例のない最大圧力1.87 GPaの精密磁化測定に成功しています。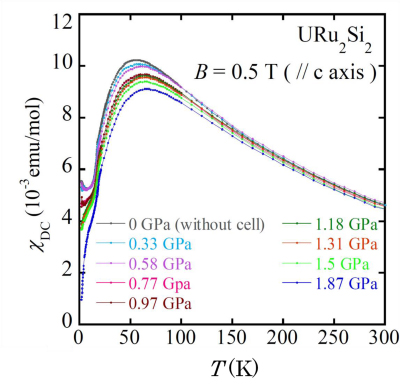
図5 URu2Si2の高圧下における磁化率の温度依存性
緩和法比熱測定
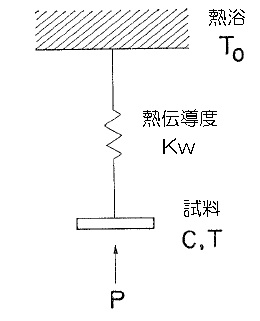
熱緩和法とは、試料に与えていた熱を切った際の試料温度の緩和現象から比熱を求める実験手法です。具体的には、試料の回りに精密に温度コントロール可能な熱浴T0を作り、試料と熱浴との間を比較的弱い熱伝導パス(熱伝導度KW)で結びます。(図1)試料部には小型の温度計とヒーターを装着し、このヒーターに通電する事で試料温度を熱浴よりΔT だけ高い定常状態で保持しておきます。その後、一気にヒーターを切ると熱伝導パスを通じて試料から熱浴に熱が逃げて行きます。この温度緩和過程は通常指数関数型になり、その時定数を解析する事により試料部の比熱を求めます。 この実験手法により、わずか数mg程度の小さな試料の比熱を広い温度範囲かつ強磁場中で測る事が出来ます。比熱からは物質のエントロピーを見積もる事ができて、系のもつ微視的自由度の振る舞いを予想できます。比熱は物質の性質を理解する上で最も重要な物理量のひとつです。我々の研究室では、Heliox :0.36 [K] < T < 200 [K] 、 B < 12 [T] (図2)
PPMS :2 [K] < T < 380 [K] 、 B < 9 [T] (図3)
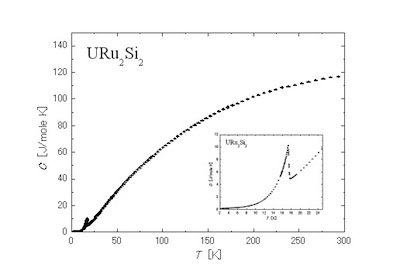
これらの装置により比熱測定を行っています。図4にPPMSでの実際の測定結果を示します。
図1 |
図2 |
図3 |
図4 |
SQUID磁束計による磁化測定

図1 Quantum Design社製MPMS
Quantum Design社製のMPMS(Magnetic property Measurement System) (図1) は取り扱いが簡便で測定感度が高い磁化測定装置です。 この装置は引き抜き法と呼ばれる方法を用いて磁化を求めています。引き抜き法とは図2のようなコイルの中で磁化した試料を引き抜きコイルに発生した誘導起電力を測定、フィッティングすることで磁化を求める方法です。コイルが上下と中心で逆向きになっていることで外部の磁場の干渉やノイズを除去することができます。 MPMSで測定できる温度は2~400 K、印加できる磁場は-5.5 T~5.5 Tです。また圧力セルを用いることで高圧下での磁化測定、回転機構を用いることで角度分解磁化測定といった測定も可能になります。|
図2 引き抜き法の概念図 |
図3 試料の位置に対する誘導起電力とフィッティング関数 |
Topics: Double ultrasonic dispersions due to rattling in SmOs4Sb12
|
Magnetic-Field-Independent Ultrasonic Dispersions due to Rattling in the Magnetically Robust
Heavy Fermion System SmOs4Sb12 Tatsuya YANAGISAWA, Yoichi IKEDA, Hitoshi SAITO, Hiroyuki HIDAKA, Hiroshi AMITSUKA, Koji ARAKI, Mitsuhiro AKATSU, Yuichi NEMOTO, Terutaka GOTO, Pei-Chun HO, Ryan E. BAUMBACH, and M. Brian MAPLE |
Elastic properties of the filled skutterudite compound SmOs4Sb12 have been investigated by ultrasonic measurements. The elastic constant C12(\omega) shows two ultrasonic dispersions at ∼15 K and ∼53 K for frequencies \omega between 33 and 316 MHz, which follow a Debye-type formula with Arrhenius-type temperature-dependent relaxation times, and remain unchanged even with applied magnetic fields up to 10 T. The corresponding activation energies were estimated to be E2 = 105 K and E1 = 409 K, respectively. The latter, E1, is the highest value reported so far in the Sb-based filled skutterudites. The presence of magnetically robust ultrasonic dispersions in SmOs4Sb12 implies a possibility that an emergence of a magnetically insensitive heavy fermion state in this system is associated with a novel local charge degree of freedom which causes the ultrasonic dispersion. J. Phys. Soc. Jpn. 80 (2011) 043601. (also available on cond-mat/1010.1387)
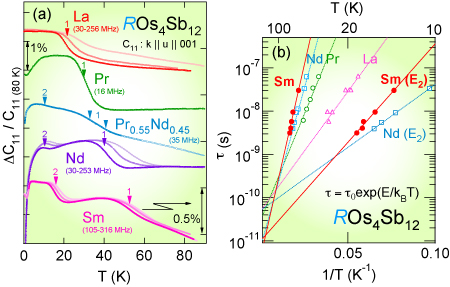
Figures (a) Comparison of the ultrasonic dispersions that appear in elastic constant C11 of ROs4Sb12 (R = La-Sm) at several frequencies. Lower arrowheads with numbers 1 and 2 indicate the relaxation point \omega\taui ∼ 1 for i = 1 and 2, respectively. (\omega is ultrasonic frequency and \tau is relaxation time) The displayed data have been shifted to eliminate overlapping with each other and the SmOs4Sb12 data are magnified three times for the \Delta C11/C11-axis. (b) Arrhenius plots of the characteristic parameters of the ultrasonic dispersions (Attempt time: \tau0(i), Activation Energy: Ei) for ROs4Sb12 (R = La-Sm). (*This research was performed at UC San Diego, Hokkaido University, and Niigata University in 2010.) |