Researches

Nuclear Magnetic Resonance: NMR

A material is composed of nuclei and electrons. The nuclei form a lattice to sustain the material, and the electrons surrounding nuclei are responsible for the properties of materials, such as magnetism and conductivity. We utilize, for the Nuclear Magnetic Resonance (NMR) experiment, the nuclei as the microscopic probe to sense the diverse properties of electrons.

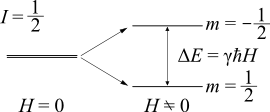Let us assume, for simplicity, a nucleus with a nuclear spin of I = 1/2. When this nuclear spin is situated under a magnetic field H₀, the energy levels of up spin (m = 1/2) and down spin (m = -1/2) split due to the Zeeman interaction H_Z = -γℏHI. A resonance occurs between this Zeeman split nuclear spin and electromangetic wave with the frequency equivalent to the energy difference ΔE = E_1/2 - E_-1/2 = -γℏH₀.

This resonance condition (ω = -γH₀) is modified by the environment around the target nuclei. We have the greatest interest in the modification derived from the electrons, namely conduction electrons.

Static contribution

The magnetic flux density in a material is the sum of that supplied by external magnetic fields and that induced by magnetization of the material. This additional magnetization term changes the energy levels of nuclear spins, and gives a static shift in the resonant frequency.

In a case of nomal metal, where the conduction electrons give rise to the Pauli paramagnetic susceptibility, temperature independent NMR shift is observed. Whereas in a paramagnetic state of ferromagnet, the NMR frequency shift follows the Curie-Weiss temeprature dependence as in the case of static susceptibility.

In addition to the electron spin contribution, orbital current can create the additional magnetic flux density at the nuclear site. This so-called "chemical" shift provides precious information on the chamical bonding, and is used to identify the chemical structure.

Dynamic contribution

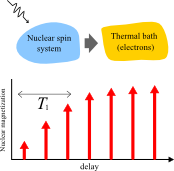Once the nuclear spins are excited by rf fields, they relax to the thermal equilibrium state releasing the supplied energy. For the relaxation process, a thermal bath, which can accept the released energy, is required, and the nature of the thermal bath determins the typical time scale for the nuclear spins to be relaxed.

Inversely, The nuclear spin relaxation time measurement allows us to deduce the properties of thermal bath, which is, in most of the cases, the electron spin system. We take advantage of the dynamical information obtained by relaxation time measurement to investigate the characters of enhanced spin fluctuations in the vicinity of magnetic instability.

These two features are the most fundamental application of NMR. We try to eplore farther possibility of this microscopic experimental technique.