[TOPICS] カゴ状化合物のラットリングとトンネリング
T. Yanagisawa et al.: J. Phys. Soc. Jpn. 80 (2011) 043601.
T. Yanagisawa et al.: J. Phys. Soc. Jpn. 77 (2008) 074607.
1.研究の背景
まずは、図1をごらんください。左側に見えるのは幼児や猫が遊ぶ「ガラガラ」(英語では"Rattler" ラトラー)と呼ばれるおもちゃです。カゴ状の容器の中に鈴やボールが内包されています。「ラットリング」とは「ガラガラと音を鳴らす」という意味の英単語です。ガラガラ蛇のことも英語では"Rattle Snake"と呼びますね。
右にも似たようなカゴがあります。こちらは原子のカゴです。このようなカゴ状の結晶構造を持つ化合物は数多く知られています。原子のカゴの大きさはたかだか数ナノメートル(~0.000000001 m)。結晶の中においてはこれらの原子のカゴは規則的に並んでいます。原子のカゴの中をよく見ると、1つの原子が内包されています。図1の右に示した三つの物質に於いては、この内包原子が中心から外れた位置(オフセンター位置)を運動していると考えられています。このミクロな原子のガラガラ運動も、左のガラガラおもちゃと類推して「ラットリング」と呼びます。
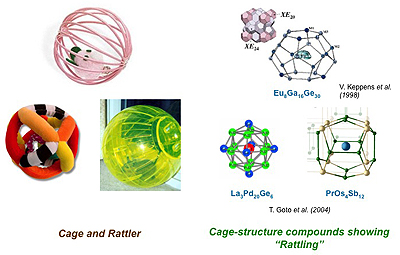
図1 幼児や猫が遊ぶ玩具「ガラガラ」(左)と内包イオンを持つ原子のカゴ(右)
図1の右下にあるPrOs4Sb12という物質は、充填スクッテルダイト化合物と呼ばれる物質で、ラットリングを示すカゴ状化合物です。Os(オスミウム)原子が4つとSb(アンチモン)原子12個から構成されるカゴの中に、希土類元素(レアアース)のPr (プラセオディウム)原子(金属化合物なので正確にはイオン)が内包されています。2004年に後藤(新潟大)らよってPrOs4Sb12のラットリングが観測されて以来、原子カゴに内包された希土類イオンの局所振動と、電子系との強相関によって生じる局所電荷ゆらぎがもたらすエキゾチックな物性が注目され、カゴ状化合物を対象に「ラットリング」をキーワードにした研究の扉が開かれました。[1] それ以前にもMaple(UC San Diego)らによってPr化合物で初の重い電子超伝導、磁場誘起四極子秩序など多彩な物性を示すことが報告され非常に注目されてきた物質です。[2] また、充填スクッテルダイト化合物の物質群 RT4X12 (R = 希土類, T = Fe, Ru, Os, X = P, As, Sb)は、文部科学省の特定領域研究「充填スクッテルダイト構造に創出する新しい量子多電子状態の展開」によって日本国内で精力的に研究が推進されてきました.以上の研究背景を鑑み、我々はPrOs4Sb12のラットリングに起因するエキゾチックな物性を探索するために類似物質NdOs4Sb12を研究ターゲットに選びました。次に結晶構造を詳しくみてみましょう。
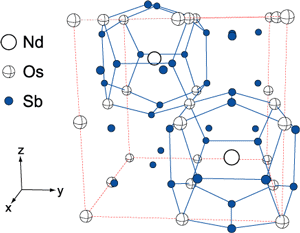
図2 充填スクッテルダイトNdOs4Sb12 のカゴ状構造
図2はNdOs4Sb12の結晶構造です。[3] 赤い四角は単位格子を示しています。カゴは[11-1]方向にOsを介して周期的に連なっており、カゴの中にはNd(ネオジウム)イオンが内包されています。重要な点は、図1に示したおもちゃのガラガラは自由にカゴの中を移動できますが、充填スクッテルダイトのような金属化合物の原子カゴの中の内包イオンは、カゴを形作っている原子としばしば強い相互作用をするという点です。
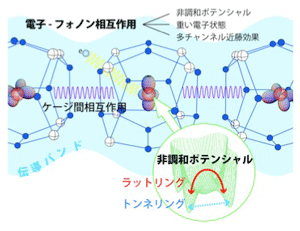
図3 充填スクッテルダイトにおける局所フォノンと伝導電子との相互作用の模式図
図3は電子と局所フォノンの相互作用の概念図を示しています。カゴの中で局所振動する希土類イオンと周囲の伝導電子との間に働く強い電子-フォノン相互作用は、カゴ中に非調和ポテンシャルを作り出します。その結果オフセンター位置に電荷ゆらぎが生じ、カゴに内包された希土類イオンはポテンシャルの対称性を反映した縮退量子状態を持つことになります。
「ラットリング」の描像については、残念ながら学会でも未だコンセンサスが得られていません。ここであらかじめ「ラットリング」という言葉を再定義しておきましょう。本解説では「ラットリング」とは、「オフセンター電荷分布を持つイオンの縮退量子状態から熱励起によってポテンシャル障壁を飛び越し、準安定状態への遷移を経て再びオフセンター状態に戻る熱活性運動」と定義します。[4]
この熱活性運動は然るべき温度で超音波分散を引き起こすため、弾性定数の周波数依存性として観測することができます。さらに低温ではラットリングの熱活性運動が死に絶えた後、ポテンシャル障壁を量子力学的に透過するトンネリング運動が姿を現します。トンネリングは低温で弾性定数のソフト化を引き起こします。局所振動するイオンは周りの伝導電子を媒介した(RKKY的な)相互作用により隣のカゴと反強的な相互作用をしていることが弾性定数の解析から判明しており、量子状態が縮退を解かず絶対零度近傍までオフセンターの揺らぎが残っている可能性があります。このような金属中のイオンの局所フォノンと伝導電子系の強結合がもたらす物性研究は、古くはA15化合物におけるYuとAndersonの理論研究に始まる固体物理の基本問題[5]に繋がります。近年ではCoxらによる多チャンネル近藤効果の提唱[6]、 三宅ら・大野らの理論計算による電子-フォノン相互作用起源の重い電子系[7,8]などへと発展を遂げました。これらの基本問題を踏まえ、我々の研究では電荷ゆらぎをともなうラットリングに由来する重い電子超伝導と磁性の共存の機構解明を目指しています。
2。 測定原理
超音波はラットリング・トンネリングを観測する絶好のプローブです。その理由は、超音波として固体内を伝搬する「歪み場」が、オフセンター振動に起因する「異方的電荷分布」と結合する性質がある所為です。図4は我々が実際に物理量を測定する際に試料に入力(input)する「外場」と、それに応答(response)する「自由度」、実際に観測される(output)「物理量」の対応表を示します。
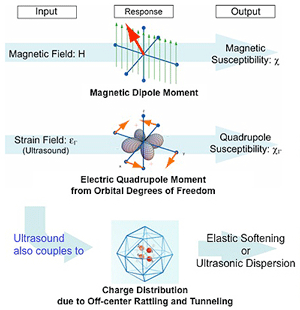
図4 超音波と結合する自由度(磁気感受率との類推)
超音波測定は、よく知られた磁化や帯磁率などの磁気測定と類推することができます。ここで、磁気測定に於ける「磁場」は、超音波測定では「歪み場」となります。それぞれに応答する自由度は、磁場に対しては電子の持つスピン自由度を反映した「磁気双極子モーメント(Magnetic Dipole Moment)」、歪み場に対しては電子の持つ軌道自由度を反映した「電気四極子(Electric Quadrupole Moment)」です。これらは実際の物理量として磁気感受率(帯磁率)、四極子感受率(弾性定数)として観測されます。
本研究で注目するラットリングやトンネリング等のイオンの局所振動は、局所オフセンタ電荷分布(Local Off-center Charge Distribution)として電気四極子と同様に超音波でとらえることができます。もし、この局所電荷分布が然るべき対称性を持っている場合は、同じ対称性の歪みに対応した然るべき超音波モードに応答が現れます。

図5 研究室で合成した充填スクッテルダイトNdOs4Sb12 の単結晶
超音波実験には単結晶試料が必要です。我々はフラックス法を用いて、石英管の中に原料を封入し、電気炉の中で1050℃に熱して溶融させ、それを約2週間かけて除冷することで図5の写真のような美しい結晶を得ることができました。充填スクッテルダイトNdOs4Sb12はTFM ~ 0.9 Kで強磁性転移を示し、比熱から見積もられる電子比熱係数γ ~ 520 mJ/mol K2 (m* ~ 98m0)と大きく、重い電子的振る舞いを示唆していますが、最近行われたドハース・ファンアルフェン効果から見積もられた有効電子質量は比較的軽いという報告がなされており、矛盾した結果が示されています。三宅らの提唱したオフセンター振動起源の準粒子質量の増強の可能性を探るべく、本研究では弾性定数を測定し、ラットリングの検証を行いました。[9]
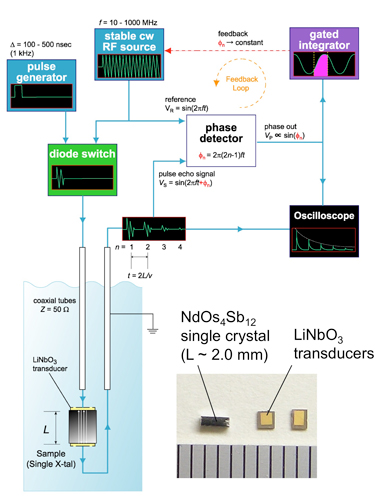
図6 超音波パルス位相比較法による音速測定装置の概念図
図6に超音波測定の原理図を示します。[10] 左上にある水色と黄緑色の装置で周波数10メガヘルツ - 1ギガヘルツ、幅100 - 500 ナノ秒のパルス信号を発生させ、同軸管で冷凍機内部にある試料まで伝送します。電気信号は試料の表面に接着された圧電素子(LiNbO3)によって超音波に変換され、試料内部を伝搬し端面で何度も反射を繰り返します。試料のもう一方に接着された圧電素子は超音波を再び電気信号に変換し、オシロスコープと位相検出器(Phase Detector)に入力されます。位相比較器は試料を通った信号と試料を通らずにそのまま入力される信号の位相差を検出し、その位相差を一定にするように始めの信号発生装置へ負帰還をかけます。
超音波の周波数変化Δf/fは、試料内部の音速の相対変化Δv/vと比例関係にありますので、信号発生器の周波数変化を読み取ることによって、音速の相対変化に読み替えることができます。弾性(スティフネス)定数はモノの堅さの指標で、物質の密度×音速の自乗(C = ρv2)の関係があります。
3.実験結果 充填スクッテルダイトNdOs4Sb12のラットリング
次に、実際の実験結果を説明します。
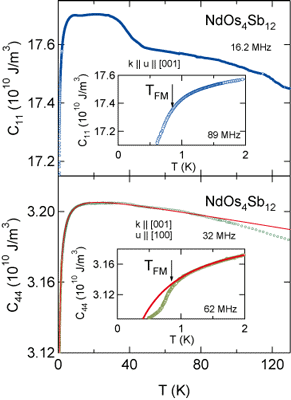
図7 NdOs4Sb12の縦波弾性定数C11と横波弾性定数C44の温度変化
図7は縦波弾性定数C11と横波弾性定数C44の温度変化を示しています。挿入図は低温領域(強磁性転移近傍)の拡大図です。両方の超音波モードは共に高温側からゆるやかに弾性定数が増加する標準的な振る舞いを示し、10 K付近から急激に減少(ソフト化)しています。このソフト化は結晶場効果として理解できます。C44にオーバーラップして表示されている赤色の実線は、Nd3+イオン(J = 9/2)の局在4f電子の結晶場基底状態をΓ67(2)四重項と仮定した場合の四極子感受率の計算結果であり、実験結果を良く説明しています。群論の選択則からΓ5二重項を結晶場基底状態に仮定した場合はソフト化が起こり得ないため、本研究の弾性定数C44の結果から結晶場基底状態を判定できました。[11]
一方、弾性定数C11には45 Kと15 K付近に特徴的なくぼみと上昇が見られます。これはラットリングに起因する超音波分散であると考えられます。次に詳しく見ていきましょう。
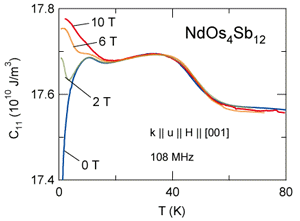
図8 NdOs4Sb12の縦波弾性定数C11の温度変化の磁場依存性
図8はNdOs4Sb12の縦波弾性定数C11の温度変化の磁場依存性を示します。零磁場で低温領域に見られた結晶場効果に起因するソフト化は磁場印加に伴い抑制され、 強磁性相境界と一致する温度で極小を示しています。 45 Kと15 K付近に見られる特徴的な上昇とくぼみは10 Tの磁場を印加しても全く影響を受けず、零磁場と同様の周波数依存性を示します。横波弾性定数C44モードも同じ温度領域で超音波分散を示しますが、その相対変化量はC11と比較しても1/20と小さく(図省略)、C11が超音波分散に対して支配的だと言えます。先にR3Pd20Ge6(R = La, Ce, Pr, Nd), ROs4Sb12 (R = La, Pr)に於いて発見された超音波分散との類推から、NdOs4Sb12が示すこの超音波分散もラットリングが起源であると結論できます。
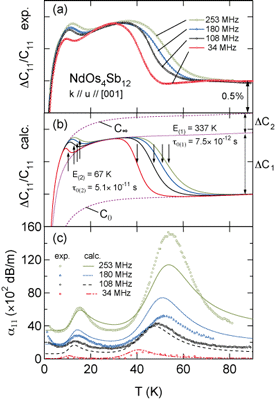
図9 NdOs4Sb12のラットリングに伴う超音波分散 (a) 縦波弾性定数C11の温度変化の周波数依存性、(b)理論曲線、(c)超音波吸収係数α11の周波数依存性
図9は零磁場における超音波分散の周波数依存性です。(a)は弾性定数C11の周波数依存性、(c)は超音波吸収係数α11の周波数依存性です。本物質は2つの超音波分散を示すため, Debye型の緩和式において2組の特性時間τ0,(i)と活性エネルギーEi (i = 1,2)を変数として用いることで解析を試みました。アレニウス型の緩和時間の温度依存性τi = τ0,(i)exp(Ei/kT)を仮定し、低温側(15 K)と高温側(45 K)の2ヶ所の超音波分散の解析から得られた2組の変数(τ0,(i), Ei)はそれぞれ, (τ0,(1) = 7.5×10-12 s, E1 = 337 K), (τ0,(2) = 5.1×10-11 s, E2 = 67 K)となりました。
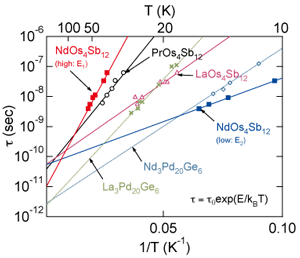
図10 ラットリングを示す類似物質の緩和時間のアレニウスプロット
これらの変数を温度の対数でプロットしたのが図10です。比較のために、これまでにラットリングが報告されている充填スクッテルダイト化合物LaOs4Sb12, PrOs4Sb12と,クラスレート化合物La3Pd20Ge6, Nd3Pd20Ge6のラットリング変数も同様に示してあります。[12] NdOs4Sb12の高温側の分散(E1)から得られた変数を比較すると、スクッテルダイト系における系統的な変化(La→Pr→Nd)が見られます。一方、低温側の分散(E2)から得られた変数は比較的遅い緩和時間を持ち、クラスレート化合物に近い値を示していることがわかります。他の物理量と比較することでラットリング機構の解明に繋がることが期待できます。
4.Γ23オフセンターモード
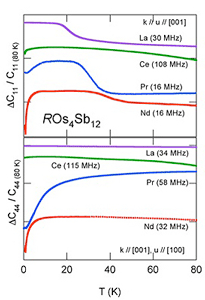
図11 充填スクッテルダイトROs4Sb12(R = La, Ce, Pr, Nd)の弾性定数C11とC44の比較[13]
図11に示すように、ROs4Sb12 (R = La, Pr, Nd)の超音波分散は弾性定数C11と(C11-C12)/2に対して支配的であり、弾性定数C44にはほとんど現れません。これは超音波分散の原因であるラットリングが対称性を伴う運動であることを示唆しています。弾性定数C11はC11= CB+4/3*(C11-C12)/2と分解でき、Γ1対称性のバルクモジュラスCBとΓ23モードの(C11-C12)/2の成分を両方含みます。また、PrOs4Sb12ではピュアなΓ23モードである弾性定数(C11-C12)/2の観測に成功しており、より明瞭な超音波分散を示します。(図省略)これらの実験結果からROs4Sb12 のラットリングはΓ23対称性に関係する電荷揺らぎを伴っていると推測されます。Γ23対称性の起源は局所振動する希土類イオンが感じる非調和ポテンシャルの形によると考えられます。原子のカゴの幾何学的な配置に立ち戻って考えてみましょう。
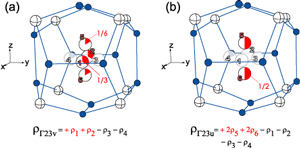
図12 [001]方向に六配位を仮定した場合のΓ23モード・オフセンター電荷分布((a) ρΓ23v (b)ρΓ23u)
図12に充填スクッテルダイトのカゴ状構造と、Γ23対称性の電荷分布の概念図を示します。充填スクッテルダイトROs4Sb12の原子カゴ(OsSb3)4は、中央の希土類サイトから見ると、[111] 方向に遷移金属のOsが位置しています。 ここで、(Osを避ける方向の)6つの[100]方向にオフセンター極小があると仮定し、オフセンター位置の電荷分布を希土類サイトの点群Thにおいて既約分解すると、Γ1+ (+)Γ23+(+)Γ4-となります。(ここで上付きの"+"と"-" は空間反転対称性のパリティを示す。"(+)"は直和で、通常の記号は○の中に+を入れたもの。) Γ23モードのオフセンター電荷分布はρΓ23v= ρ1+ρ2-ρ3-ρ4 とρΓ23u=2ρ5+2ρ6-ρ1-ρ2 の二種類あります。図12には円グラフで各オフセンター位置の電荷を図示してあります。[1] これら二つの電荷分布はエネルギー的に等価であるため、量子状態は二重縮退しています。極低温において、この縮退量子状態間をトンネリングすることによって、弾性定数にソフト化が現れます。このトンネリングに起因するソフト化はLaOs4Sb12の極低温領域や、PrOs4Sb12の重い電子超伝導転移点直上において観測されており、これまでの実験からLaOs4Sb12のソフト化は16 Tの強磁場下でも全く影響を受けることなく、20 mKの極低温までソフト化が停止しないことが解っています。[12]
5. エピローグ
ここでBCS超伝導を示すLaOs4Sb12(TSC = 0.74 K)と、重い電子超伝導を示すPrOs4Sb12(TSC = 1.85 K)の超伝導転移点における弾性定数の振る舞いの違いについて少し触れます。BCS超伝導体のLaOs4Sb12はTSCにおいてアノマリーを示さず20 mKの極低温までトンネリングに起因するソフト化を示すのに対し、非BCS超伝導のPrOs4Sb12はTSC直上からトンネリングに起因したソフト化が生じ、TSCで停止します。(図省略)これら二つの物質のTSCにおける弾性定数の振る舞いの明確な差異は、オフセンター自由度が重い電子超伝導に寄与している可能性を示唆しています。またPrOs4Sb12に現れた弾性定数の極小は、超伝導転移に伴う縮退量子状態の分裂、即ちPrOs4Sb12の重い電子超伝導相におけるSymmetry Breaking(対称性を破る)な性質を暗示しています。
残された課題は希釈系におけるラットリング・トンネリングの検証です。BCS超伝導と非BCS超伝導がクロスオーバーする領域におけるオフセンター自由度の寄与を明らかすること(例 Pr1-xLaxOs4Sb12)と、NdOs4Sb12のラットリングが示す2つの異なる活性エネルギーの起源の解明(例 Pr1-xNdxOs4Sb12)です。これら二つの問題を解決すべく研究を継続しています。(文責 柳澤)
[1] T. Goto et al., Phys. Rev. B 69 (2004) 180511(R).
[2] M.B. Maple et al., J. Phys. Soc. Jpn. 71 (2002) Suppl. 23.
[3] D.J. Braun and W. Jeitschko, J. Less-Common Metals 72 (1980) 147.
[4] T. Goto et al., Phys. Rev. B 70 (2004) 184126.
[5] C. C. Yu and P. W. Anderson, Phys. Rev. B 29 (1984) 6165.
[6] D. L. Cox, Phys. Rev. Lett. 59 (1987) 1240.
[7] K. Mitsumoto and Y. Ono, Physica C 426-431 (2005) 330.
[8] K. Hattori et al., J. Phys. Soc. Jpn. 74 (2005) 3306.
[9] P. C. Ho et al., Phys. Rev. B 72 (2005) 094410.
[10] B. Luethi: Solid State Sciences,
Physical Acoustics in the Solid State (Springer Berlin Heidelberg, New York, 2005) Vol. 148.
[11] T. Yanagisawa et al., J. Magn. Magn. Mater. 310, 223 (2007).
[12] Y. Nemoto et al.,
J. Phys. Soc. Jpn. 77 (2008) Supplement A, pp. 153-158.


